Егэ-тренер. Подготовка 2022-2023
Тренинги в прямом эфире для учителей и учеников

С4. Доказательства, часть 5

Дата: 2014-03-14 20:00:00

В данной подборке собраны нелёгкие задачи, связанные с высотой треугольника.

1) Высоты остроугольного треугольника АВС пересекаются в точке О. Докажите, что
радиусы окружностей, описанных около треугольников ABС и ОВС равны.

2) Доказать, что отрезок, соединяющий основания высот треугольника,
отсекает от него подобный ему треугольник.

3) Пусть в остроугольном треугольнике ABC точки A₁, B₁, C₁ - основания высот. Докажите,
что точка О пересечения высот треугольника ABC является точкой пересечения
биссектрис треугольника A₁B₁C₁.

4) Доказать что расстояние от ортоцентра до вершины треугольника в два раза
больше расстояния от центра описанной окружности до сторон.

В планиметрических задачах появилось недавно новшество - пункт а) - задание на доказательство.
С одной стороны, это прекрасно и даёт шанс ученику, не бравшемуся ранее за С4, получить балл.
С другой стороны, культурой правильного, грамотного доказательства владеют далеко не все.

На самой первой лекции мы взяли разгон, доказав немало знакомых (казалось бы) утверждений.
Запись лекции ждёт Вас в личном кабинете. Она Вам понравится и облегчит жизнь, учитесь ли Вы или
преподаёте сами. Подбор задач и подход к ним тщательно продуманы для первого знакомства.

На второй лекции мы продолжили учиться правильно использовать и записывать слова и термины.
На третьей лекции задачи стали ещё сложнее и ещё интереснее.

                                                    

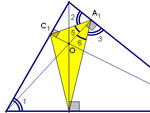
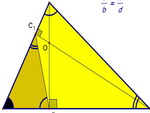
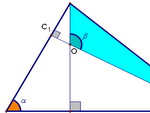Не пропустите этот важный для Вас курс, не стоит "забивать" на планиметрию, есть время научиться!