Егэ-тренер. Подготовка 2022-2023
Тренинги в прямом эфире для учителей и учеников

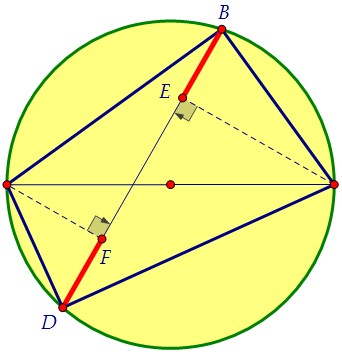
С4. Доказательства, часть 3

Дата: 2013-10-29 19:30:00

Задачи, которые разбираются на лекции. Решите их заранее, Вам будет интереснее!

1) Докажите, что если диагонали трапеции равны, то трапеция равнобедренная.

2) Через середину O гипотенузы AB прямоугольного треугольника ABC проведена
прямая, перпендикулярная AB, и на этой прямой в обе стороны от точки O отложены
отрезки OD и OE, равные половине гипотенузы. Докажите, что CD и CE – биссектрисы
внутреннего и внешнего углов треугольника ABC при вершине C.

3) Одна из диагоналей вписанного в окружность четырёхугольника является диаметром.
Докажите, что проекции противоположных сторон на другую диагональ равны.

4) На диагонали BD параллелограмма ABCD взята точка K. Прямая AK пересекает
прямые BC и CD в точках L и M. Докажите, что AK² = LK · KM.

5) Через точку O проведены три прямые, попарные углы между которыми равны 60°.
Докажите, что основания перпендикуляров, опущенных на эти прямые из произвольной
точки M, служат вершинами правильного треугольника.

6) Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки
АВ и СЕ равны.

В планиметрических задачах появилось недавно новшество - пункт а) - задание на доказательство.
С одной стороны, это прекрасно и даёт шанс ученику, не бравшемуся ранее за С4, получить балл.
С другой стороны, культурой правильного, грамотного доказательства владеют далеко не все.

На самой первой лекции мы взяли разгон, доказав немало знакомых (казалось бы) утверждений.
Запись лекции ждёт Вас в личном кабинете. Она Вам понравится и облегчит жизнь, учитесь ли Вы или
преподаёте сами. Подбор задач и подход к ним тщательно продуманы для первого знакомства.

На второй лекции мы продолжили учиться правильно использовать и записывать слова и термины.
К третьей лекции задачи потихоньку усложняются и становятся всё интереснее и интереснее.



Не пропустите этот важный для Вас курс, не стоит "забивать" на планиметрию, есть время научиться!