Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Через точку внутри треугольника проведены три прямые, параллельные сторонам (вар. 83)
Комментарии к этой задаче: Комментарий добавил(а): Михаил Н. Эта задача проще решается. Почти устно. Используя рисунок предыдущего решения, обозначим: AE=x, EF=x, FC=z. Далее: S1/S=(x/(x+y+z))^2, аналогично, S2/S=(y/(x+y+z))^2 и S3/S=(z/(x+y+z))^2. Остается извлечь корни из этих равенств, сложить и получить ответ Комментарий добавил(а): Ольга Себедаш Михаил, быстро написать - не значит быстро и просто решить. Моё решение большей частью объясняет саму идею. А само решение в пару строчек записать легко)) Добавить Ваш комментарий: |

 Нам надо доказать весьма замысловатую формулу, запишем её и расшифруем:
Нам надо доказать весьма замысловатую формулу, запишем её и расшифруем: Поделив равенство на два, слева получим сумму площадей треугольников:
Поделив равенство на два, слева получим сумму площадей треугольников: Таким образом, доказать надо следующее равенство:
Таким образом, доказать надо следующее равенство: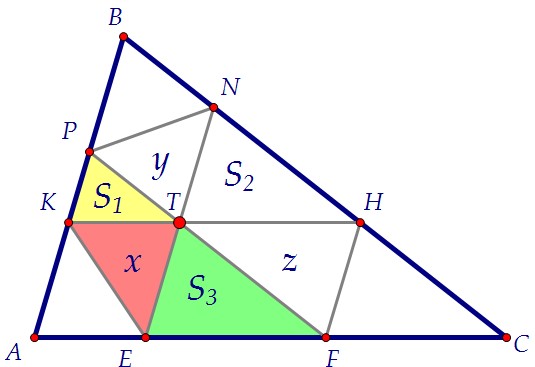 Рассмотрим и опять же расшифруем первое равенство:
Рассмотрим и опять же расшифруем первое равенство: