|
Через точку T внутри треугольника АВС проведены три прямые k, l и m так, что k || AB, l || BC, m || AC. Эти прямые образуют со сторонами треугольника три треугольника, два из которых равны по площади.
а) Докажите, что квадрат суммы квадратных корней из площадей треугольников, образованных прямыми k, l и m со сторонами треугольника ABC, равен площади этого треугольника;
б) Найдите площадь меньшего треугольника, если известно, что площадь треуг. ABC равна 25, а площадь каждого из равных треугольников равна 4.
Понятно, что если формула пункта а) будет доказана, то подставить в неё данные из пункта б) не составит труда. Однако решим автономно пункт б).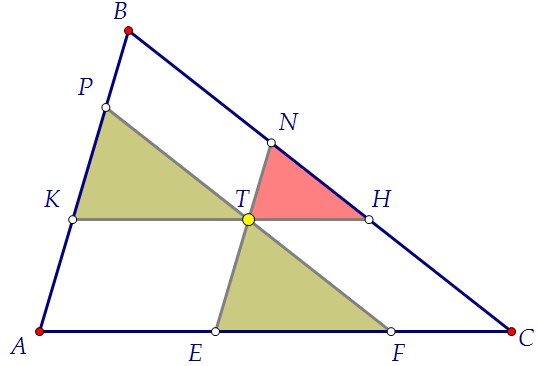 У треугольников на рисунке стороны соответственно параллельны друг другу. Несложно доказать, что они подобны по двум углам. Если площади подобных треугольников равны, то и сами треугольники тоже равны (докажите это).
У треугольников на рисунке стороны соответственно параллельны друг другу. Несложно доказать, что они подобны по двум углам. Если площади подобных треугольников равны, то и сами треугольники тоже равны (докажите это).
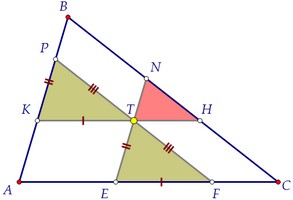 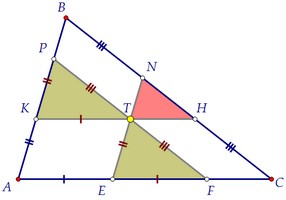 У равных треугольников по определению равны соответствующие стороны.Отмечаем ещё пары равных сторон, учитывая свойства параллелограмма.Таким образом, КТ - средняя линия треугольника APF по определению.Площадь треугольника APF в 4 раза больше площади треугольника КРТ.***Треугольники подобны с коэффициентом подобия, равным двум. У равных треугольников по определению равны соответствующие стороны.Отмечаем ещё пары равных сторон, учитывая свойства параллелограмма.Таким образом, КТ - средняя линия треугольника APF по определению.Площадь треугольника APF в 4 раза больше площади треугольника КРТ.***Треугольники подобны с коэффициентом подобия, равным двум.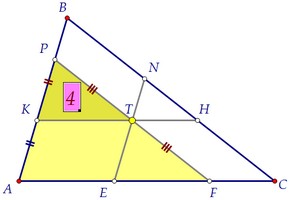 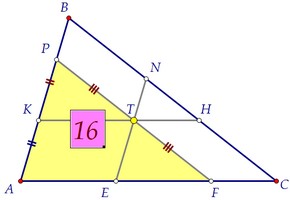 Треугольники APF и AВС тоже подобны. Их площади равны 16 и 25.Значит, соответствующие стороны треугольников относятся, как 4 : 5.Учитываем заодно равенство противоположных сторон параллелограмма: Треугольники APF и AВС тоже подобны. Их площади равны 16 и 25.Значит, соответствующие стороны треугольников относятся, как 4 : 5.Учитываем заодно равенство противоположных сторон параллелограмма: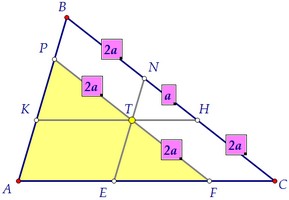 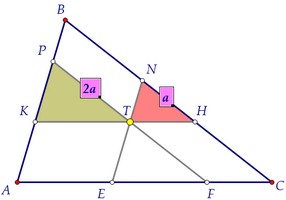 Наконец, замечаем ещё одну пару подобных треугольников: KPT и TNH.Коэффициент подобия равен 2, значит, площади относятся, как 4 : 1.Таким образом, площадь маленького треугольника TNH равна 1.Ответ:1 Наконец, замечаем ещё одну пару подобных треугольников: KPT и TNH.Коэффициент подобия равен 2, значит, площади относятся, как 4 : 1.Таким образом, площадь маленького треугольника TNH равна 1.Ответ:1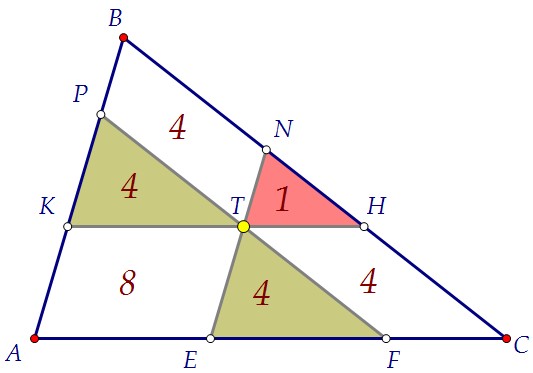 Доказать утверждение пункта а) можно, рассуждая аналогично, обозначив данные равные площади через х, используя те же подобия и отношения.Но на следующей странице утверждение будет доказано в общем виде, то есть точка внутри треугольника произвольная, наличие равных треугольников необязательно. Доказать утверждение пункта а) можно, рассуждая аналогично, обозначив данные равные площади через х, используя те же подобия и отношения.Но на следующей странице утверждение будет доказано в общем виде, то есть точка внутри треугольника произвольная, наличие равных треугольников необязательно. Автор: Ольга Себедаш Просмотров: 11257
|

