|
Смотреть видеоурок
Решите неравенство:
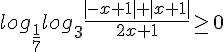
Рассмотрим это интересное неравенство как самостоятельную единицу.
Ниже, после решения я покажу, как учесть первое неравенство системы варианта 58.
=========================================
Для начала перепишем неравенство, введя временную переменную: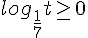 Это неравенство в силу убывания логарифма равносильно такому: Это неравенство в силу убывания логарифма равносильно такому: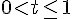 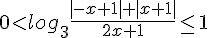 Снова временно введя переменную, запишем немного проще: Снова временно введя переменную, запишем немного проще: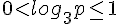 Двойное неравенство удобнее записать в виде системы:
Двойное неравенство удобнее записать в виде системы:
 В силу возрастания логарифма система равносильна системе:
В силу возрастания логарифма система равносильна системе:
 Упростим теперь само подлогарифмическое выражение:
Упростим теперь само подлогарифмическое выражение:
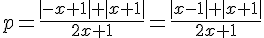 Точки -1 и 1 разбивают всю ось ОХ на три области.==========================================
1) Пусть x < -1. Тогда
Точки -1 и 1 разбивают всю ось ОХ на три области.==========================================
1) Пусть x < -1. Тогда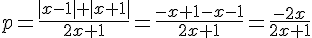 Знаменатель при этом отрицателен. Умножим на (2x + 1) < 0 каждое уравнение системы и поменяем знаки системы: Знаменатель при этом отрицателен. Умножим на (2x + 1) < 0 каждое уравнение системы и поменяем знаки системы:
 \\
\end{array} )

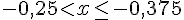 На луче x < -1 система решений не имеет.==========================================
2) Пусть x > 1. Тогда
На луче x < -1 система решений не имеет.==========================================
2) Пусть x > 1. Тогда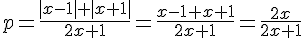 Знаменатель при этом положителен. Умножим на (2x + 1) > 0 каждое уравнение системы, знаки системы не меняем: Знаменатель при этом положителен. Умножим на (2x + 1) > 0 каждое уравнение системы, знаки системы не меняем:
 \\
\end{array} ) Не имеет решений первое неравенство, а значит, и вся система.==========================================
3) Пусть -1 ≤ x ≤ 1, х ≠ -0,5. Тогда
Не имеет решений первое неравенство, а значит, и вся система.==========================================
3) Пусть -1 ≤ x ≤ 1, х ≠ -0,5. Тогда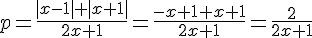 Система примет следующий вид:
Система примет следующий вид: Разобьём промежуток на две части - [-1; -0,5) и (-0,5; 1].-----------------------------------а) Пусть -1 ≤ x < -0,5. Тогда знаменатель отрицателен, и значит, p < 0. Наша система решений не имеет.-----------------------------------б) Пусть -0,5 < x ≤ 1. Тогда знаменатель положителен, умножим на него:
Разобьём промежуток на две части - [-1; -0,5) и (-0,5; 1].-----------------------------------а) Пусть -1 ≤ x < -0,5. Тогда знаменатель отрицателен, и значит, p < 0. Наша система решений не имеет.-----------------------------------б) Пусть -0,5 < x ≤ 1. Тогда знаменатель положителен, умножим на него:  \\
\end{array} )

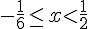 Полученный полуинтервал входит в промежуток (-0,5; 1] и является ответом.=================================
Учтём, что это неравенство было предложено с другим неравенством в системе.
Удовлетворяет ли данному неравенству х = 0, можно проверить сходу:
Полученный полуинтервал входит в промежуток (-0,5; 1] и является ответом.=================================
Учтём, что это неравенство было предложено с другим неравенством в системе.
Удовлетворяет ли данному неравенству х = 0, можно проверить сходу: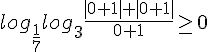 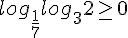 Сначала оценим внутренний логарифм (с основанием, большим единицы):
Сначала оценим внутренний логарифм (с основанием, большим единицы): 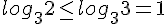 Теперь оценим внешний логарифм (с основанием, меньшим единицы):
Теперь оценим внешний логарифм (с основанием, меньшим единицы):
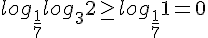 Итак, с нулём всё в порядке. Осталось проверить значения х, большие 16.Идея решения та же, но раскрывать модули достаточно лишь для х > 1.Система в этом случае (см. выше случай номер 2) решений не имеет.Таким образом, общий ответ системы только один: х = 0.
Итак, с нулём всё в порядке. Осталось проверить значения х, большие 16.Идея решения та же, но раскрывать модули достаточно лишь для х > 1.Система в этом случае (см. выше случай номер 2) решений не имеет.Таким образом, общий ответ системы только один: х = 0. Автор: Ольга Себедаш Просмотров: 12938
|
