Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
12. Сумма взаимообратных функций. Наибольшее значение на отрезке (вар. 49)
Комментарии к этой задаче: Комментарий добавил(а): dokdokay По данным Всемирной организации здравоохранения, привычка употреблять спиртное является причиной почти 4 % всех смертей в мире. От злоупотребления спиртными напитками погибает больше населения, чем от СПИДа, туберкулеза и войн. Наибольшее влияние употребления алкоголя на летальность наблюдается в РФ и странах СНГ: каждый пятый человек в них умирает от причин, связанных с употреблением спиртного Добавить Ваш комментарий: |

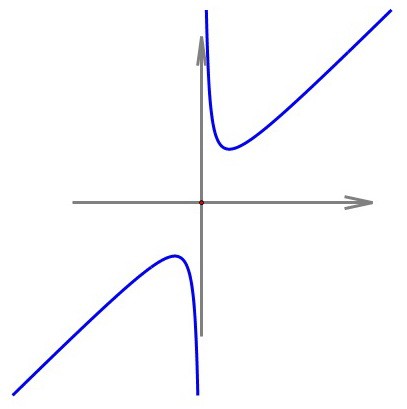 Нас интересуют отрицательные значения аргумента. Справедливо утверждение:
если произведение двух отрицательных чисел постоянно и равно а, то сумма этих чисел достигает наибольшего значения, если каждое из них равно √а.
В нашем случае произведение слагаемых равно 9, наибольшее значение
для отрицательных х достигается в т. максимума х = -3 и равно -3 - 3 = -6.
Теперь всё зависит от отрезка. Данный отрезок содержит точку х = -3, поэтомуответ: -6
Но на отрезке [-5; -4] наибольшее значение функция приняла бы в точке -4.
А на отрезке [-2; -1] наибольшее значение функция приняла бы в точке -2.
А какое наименьшее значение примет функция на отрезке [1; 5]? [1; 2]? [5; 7]?
С помощью производной при желании Вы можете исследовать функцию сами.
Нас интересуют отрицательные значения аргумента. Справедливо утверждение:
если произведение двух отрицательных чисел постоянно и равно а, то сумма этих чисел достигает наибольшего значения, если каждое из них равно √а.
В нашем случае произведение слагаемых равно 9, наибольшее значение
для отрицательных х достигается в т. максимума х = -3 и равно -3 - 3 = -6.
Теперь всё зависит от отрезка. Данный отрезок содержит точку х = -3, поэтомуответ: -6
Но на отрезке [-5; -4] наибольшее значение функция приняла бы в точке -4.
А на отрезке [-2; -1] наибольшее значение функция приняла бы в точке -2.
А какое наименьшее значение примет функция на отрезке [1; 5]? [1; 2]? [5; 7]?
С помощью производной при желании Вы можете исследовать функцию сами.