Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

12. Нахождение точки минимума функции двумя способами (вар. 44)

Найдите точку минимума функции

$y=x+\frac{324}{x}+6$

График функции можно опустить на 6 единиц вниз, и точка минимума останется на месте.

$y=x+\frac{324}{x}$

Будем искать точку минимума последней функции. Заметим, что она является нечётной.

$f(-x)=-x+\frac{324}{-x}=-f(x)$

Учитывая, что её график симметричен относительно точки О, рассмотрим сначала x > 0.

Воспользуемся следующим утверждением: если произведение двух положительных чисел постоянно
и равно а, то сумма этих чисел достигает наименьшего значения, если каждое из них равно √а.

В нашем случае оба слагаемых положительны, и их произведение постоянно и равно 324.

${x}\cdot{\frac{324}{x}}=324$

Поэтому их сумма наименьшая, если каждое слагаемое принимает значение √324 = 18.
х = 18 и есть точка минимума функции y = f(x) для положительных значений аргумента.
Так как функция нечётная, и её график симметричен относительно нуля, то точка х=-18
является точкой максимума функции. В точке 0 функция не определена и имеет разрыв.

Ответ: 18

Можно поступить и традиционным способом, исследовав функцию с помощью производной.

$y=x+\frac{324}{x}+6$

$y'=1-\frac{324}{x^2}$

$1-\frac{324}{x^2}=0$

$\frac{x^2-324}{x^2}=0$

$\frac{(x-18)(x+18)}{x^2}=0$

Две критические точки 18 и -18 и точка разрыва 0 делят ось ОХ на четыре интервала.
Определим знаки производной на каждом из этих интервалов.

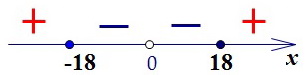Поведение функции зависит от знаков производной. Если производная положительна,
то функция возрастает. Если производная отрицательна, то функция убывает.

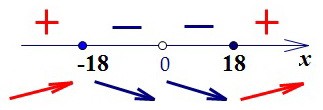Функция имеет два экстремума. В точке х = 18 убывание сменяется возрастанием.
Это и есть точка минимума функции. Точка х = -18 - точка максимума функции.
Изобразим схематически график функции

$y=x+\frac{324}{x}$