Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

14(C2). Часть 1. Построение сечения тетраэдра и поиск отношения отрезков (вар. 42)

Каждое из рёбер треугольной пирамиды ABCD имеет длину 1. Точка Р на ребре АВ,
точка Q на ребре ВС, точка R на ребре CD взяты так, что AP = 1/2, BQ = CR = 1/3.
Плоскость PQR пересекает прямую AD в точке S. Найти угол между прямыми SP и SQ.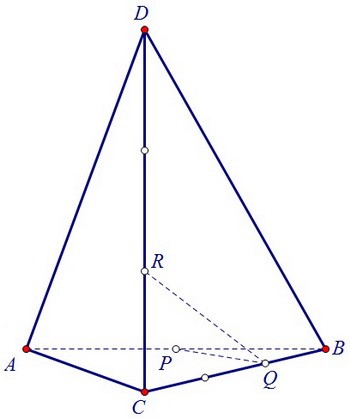

На рисунке уже соединены точки R и Q, а также P и Q - это начало построения сечения.
В плоскости ABC пересечём СА и QP, получим точку К. Она лежит к тому же в левой грани.

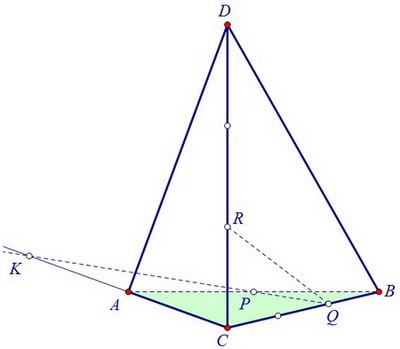В плоскости левой грани ADC пересечём отрезок KR с ребром AD, получим точку S.

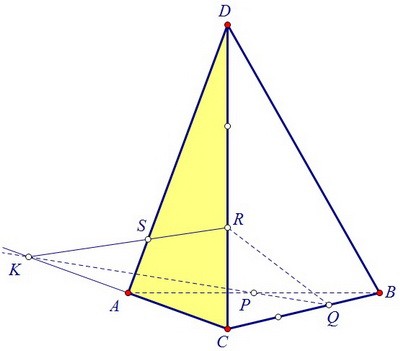Если точку S соединить с точками R и Р, то можно увидеть сечение тетраэдра SRQP.

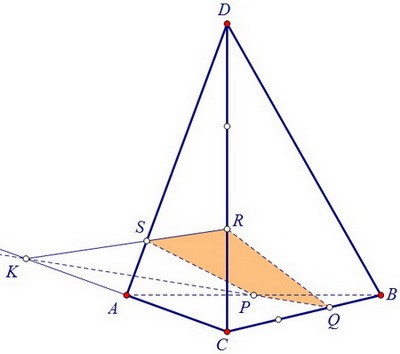Найдём, как именно расположена точка S на ребре DA, т.е. найдём длину отрезка AS.
Для этого сначала найдём длину АК. Проведём среднюю линию РЕ треугольника АВС.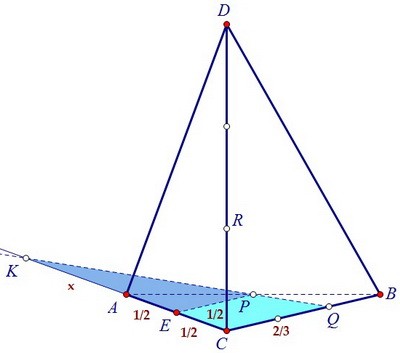

Рассмотрим подобные треугольники ЕКР и СКQ, ЕР = AE = EC = 1/2, CQ = 2/3. Пусть АК = х.

$\frac{KE}{KC}=\frac{EP}{CQ}$

$\frac{x+\frac{1}{2}}{x+1}=\frac{\frac{1}{2}}{\frac{2}{3}}$

$\frac{x+\frac{1}{2}}{x+1}=\frac{3}{4}$

$3x+3=4x+2$

$x=1$

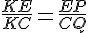
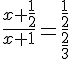
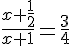
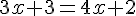
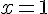Итак, АК = 1. Далее в левой грани ADC проведём RM параллельно DA, RM = 1/3.

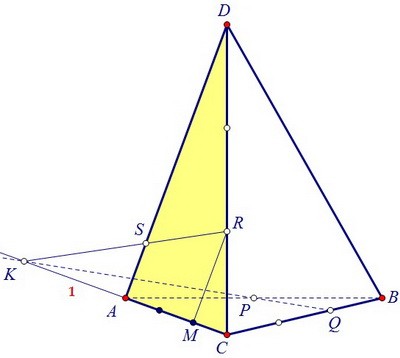Рассмотрим подобные треугольники AKS и MKR, AM = 2/3. Пусть AS = y.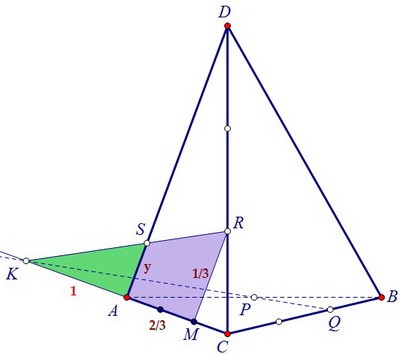

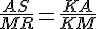
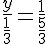
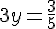
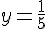$\frac{AS}{MR}=\frac{KA}{KM}$

$\frac{y}{\frac{1}{3}}=\frac{1}{\frac{5}{3}}$

$3y=\frac{3}{5}$

$y=\frac{1}{5}$

Итак, АS = 1/5. Переходим к поиску угла между прямыми SP и SQ.