Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

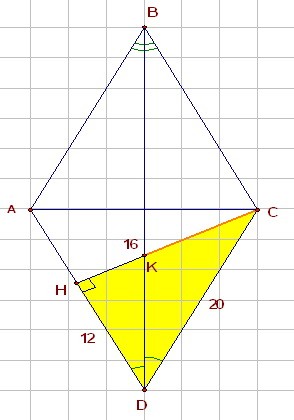
16(C4). Высота и площадь ромба

Дан ромб ABCD с острым углом В. Площадь ромба равна 320, а синус угла В равен 0,8.
Высота CH пересекает диагональ BD в точке К. Найдите длину отрезка СК.

1) Так как площадь ромба равна a2·sinB,
где а - сторона ромба, то из уравнения
a2·0,8 = 320 находим сторону ромба а = 20.
2) Зная, что sinB = 0,8 и B - острый угол,
вычисляем cosB = 0,6.
3) Заметим что в ромбе противоп. углы равны,
т.е. угол D равен углу В, и кроме того,
диагональ BD является биссектрисой угла D.
4) Из прямоуг. треугольника CHD находим
CH = a·sinD = 20·0,8 = 16, DH = a·cosD = 0,6a
(можно найти и точное значение: DH = 12).
5) В этом же треуг. применим свойство биссектрисы. Пусть СК = х, тогда HK = 16 - x.
Составим отношение:
KC
DC 		=
KH
DH		; имеем:

x
a 		=
16 - x
0,6a		; 16 - x = 0,6x; 1,6x = 16; x = 10.
Ответ: 10

Автор: Ольга Себедаш             Просмотров: 50827

Комментарии к этой задаче:

Комментарий добавил(а): венера
Дата: 2010-01-28

классно! а как найти площадь ромба, если известна наименьшая диагональ и высота ромба?

Комментарий добавил(а): вася
Дата: 2010-01-11

все понял,только уравнение сложное@)(

Комментарий добавил(а): Валентина
Дата: 2010-04-11

А как же найти sinD?

Комментарий добавил(а): Tanua
Дата: 2010-04-12

Площадь ромба равна произведению квадрата его стороны и синуса острого угла. как это доказать??????

Комментарий добавил(а): Азиза
Дата: 2010-12-23

решение задачи по геометрии:Вычислите площадь ромба,периметр которого равен 24 см,а угол,смежный с одним углом этого ромба,равен 30 градусов

Комментарий добавил(а): alina
Дата: 2010-12-27

вычислите площадь ромба, периметр которого равен 24 см,а угол, смежный с одними из углов этого ромба, равен 30 градусов

Комментарий добавил(а): Alla
Дата: 2011-05-10

сторона ромба равна 25см,а одна из диагоналей равна 48см.найдите пожалуйста площадь??

Комментарий добавил(а): Марина
Дата: 2011-05-15

Найти периметр ромба, если площадь равна 48 квадратных сантиметров, а острый угол равен 30 градусов.

Комментарий добавил(а): РОМКА
Дата: 2011-05-08

Как найти площадь ромба, если известно, что стороны равны 4см???

Комментарий добавил(а): Егэ-тренер
Дата: 2011-05-08

РОМКА, этих данных мало

Комментарий добавил(а): Саша
Дата: 2011-05-28

Найдите периметр ромба,высота которого равна 7 см,а площадь-84см.кв.

Комментарий добавил(а): анна
Дата: 2014-10-09

как нашли что косинус равен 0.6?

Комментарий добавил(а):
Дата: 2019-09-24

Добавить Ваш комментарий:
Яндекс.Метрика