Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Задача о пересечении высоты и диагонали ромба
Комментарии к этой задаче: Комментарий добавил(а): серега а откуда взялось 4/3? Комментарий добавил(а): я из COSa=0,75=34 Добавить Ваш комментарий: |

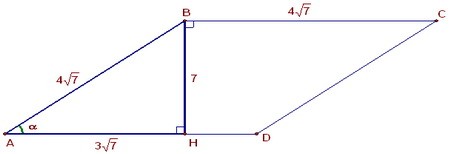 В прямоугольном треугольнике ABH: AH = AB · cosα = 4√7 · 0,75 = 3√7,
BH2 = AB2 - AC2 = 112 - 63 = 49; BH = 7.
В прямоугольном треугольнике ABH: AH = AB · cosα = 4√7 · 0,75 = 3√7,
BH2 = AB2 - AC2 = 112 - 63 = 49; BH = 7.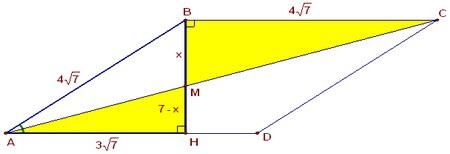 Два прямоугольных треугольника ВМС и HMA подобны по двум углам.
Два прямоугольных треугольника ВМС и HMA подобны по двум углам.