|
Определите, какое наибольшее количество общих членов может быть
у двух арифметических прогрессий 1; …; 1000 и 9; …; 999, если
известно, что у каждой из них разность является целым числом,
отличным от 1.
Чтобы совпадений было больше, разности должны быть как можно меньше.
Число 2 не может быть разностью первой прогрессии (ответьте, почему?)
Число 3 может быть её разностью. Тогда она будет выглядеть так:
1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, ... , 1000.
Каждый член прогрессии при делении на 3 даёт остаток 1.
Каждое такое число может быть записано в виде 3n + 1.
Число 2 может быть разностью второй прогрессии. Вот её вид:
9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, ... , 999.
Каждый член прогрессии при делении на 2 даёт остаток 1.
Каждое такое число может быть записано в виде 2k + 1.
Найдём арифметическую прогрессию, состоящую из общих членов.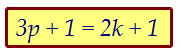
Получаем: 3p = 2k. При этом р кратно двум, а k кратно трём.
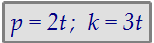Члены общей прогрессии при делении на 6 дают остаток 1.
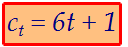Первое такое число равно 13 и имеет номер 2.
Последнее число равно 997 и имеет номер 166.
Всего таких числ 165. Автор: Ольга Себедаш Просмотров: 4024
|
