|
Определите. имеют ли общие члены две последовательности:
а) 3, 16, 29, 42, ... и 2, 19, 36, 53, ...
б) 5, 16, 27, 38, ... и 8, 19, 30, 41, ...
а) Напишем формулу n-го члена первой прогрессии
аn = 3 + 13(n - 1) = 13n - 10
Напишем формулу k-го члена второй прогрессии
аk = 2 + 17(k - 1) = 17k - 15
Решим в натуральных числах следующее уравнение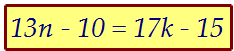
На самом деле, достаточно найти одно его решение.
13n = 17k - 5
(17k - 5) делится на 13.
Можно перебирать значения k, но... Лучше рассуждать так:
Так как (17k - 5) делится на 13,
то и (4k - 5) делится на 13
Значит, (4k + 8) делится на 13
Значит, (k + 2) делится на 13
Теперь совершенно понятно, что k = 11.
Это одно из натуральных решений.
При k = 11 аk = 17·11 - 15 = 172.
Это и есть один из общих членов прогрессии.
б) Напишем формулу n-го члена первой прогрессии
аn = 5 + 11(n - 1) = 11n - 6
Напишем формулу k-го члена второй прогрессии
аk = 8 + 11(k - 1) = 11k - 3
Решим в натуральных числах следующее уравнение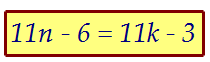
11(n - k) = 3
Очевидно, что целых решений уравнение не имеет. Автор: Ольга Себедаш Просмотров: 4070
|
