Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
19(в). Представьте число 2016 в виде суммы наибольшего количества (вар. 152)
Комментарии к этой задаче: Комментарий добавил(а): Максим А, если следовать из определения последовательного числа (Последовательное число — целое положительное число, которое может быть представлено в виде суммы двух или более последовательных натуральных чисел.), будет ли засчитан ответ: 39? Если сумма чисел начинается с 6 и заканчивается на 92, также НЕ включает в себя такие числа: 16,20,32,64 т.к. они все, кроме 20, не подходят под определение последовательного числа. Добавить Ваш комментарий: |

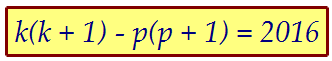 Преобразуем левую часть уравнения:
Преобразуем левую часть уравнения:
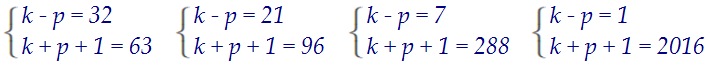 Но устраивает нас только первая, т.к. (k - p) здесь максимально.
k = 47; p = 15; k - p = 32
Таким образом, искомая последовательность состоит из 32 чисел.
Начинается эта последовательность с числа 32.
Но устраивает нас только первая, т.к. (k - p) здесь максимально.
k = 47; p = 15; k - p = 32
Таким образом, искомая последовательность состоит из 32 чисел.
Начинается эта последовательность с числа 32.