|
Найдите все значения параметра а, при каждом из которых уравнение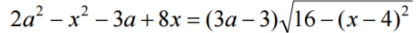 имеет ровно два различных действительных корня.
Упростим выражение под корнем справа. 16 - (x - 4)2 = 8x - x2
Это позволяет нам ввести замену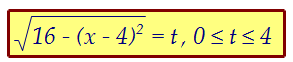
Получим квадратное уравнение относительно t:
t2 - (3a - 3)t + a(2a - 3) = 0
Для каждого t из (0, 4) получим ровно два различных значения х.
Чтобы выполнялось условие задачи, наше квадратное уравнение
должно иметь один и только один корень на интервале (0, 4).
Кроме того, необходимо проверить все граничные значения.
Рассмотрим сначала условие того, что на интервале (0, 4)
квадратное уравнение имеет один и только один корень.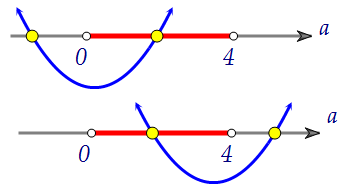 При этом значения функции f(t) = t2 - (3a - 3)t + a(2a - 3)на концах интервала (0, 4) должны иметь разные знаки: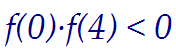
a(2a - 3)·(16 - 12(a - 1) + a(2a - 3)) < 0
a(2a - 3)·2(a2 - 15a + 28) < 0
a(2a - 3)·(a - 4)(2a - 7) < 0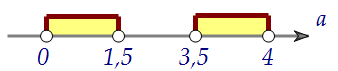
Проверим значения, при которых f(0)·f(4) = 0. Это 0; 1,5; 3,5; 4.
Проверим а = 3, при кот. корни квадратного уравнения совпадают.
====================================
Если а = 0, то корни квадратного уравнения t = 0; t = -3.
При t = 0 получаем два различных корня жёлтого уравнения.
При t = -3 жёлтое уравнение корней не имеет.
====================================
Если а = 1,5, то корни квадратного уравнения t = 0; t = 1,5.
При t = 0 получаем два различных корня жёлтого уравнения.
При t = 1,5 получаем ещё два корня.
====================================
Если а = 3,5, то корни квадратного уравнения t = 3,5; t = 4.
При t = 3,5 получаем два различных корня жёлтого уравнения.
При t = 4 получаем ещё один корень.
====================================
Если а = 4, то корни квадратного уравнения t = 4; t = 5.
При t = 4 получаем один корень жёлтого уравнения.
При t = 5 жёлтое уравнение корней не имеет.
====================================
Если а = 3, то корень квадратного уравнения один t = 3.
При t = 3 получаем два различных корня жёлтого уравнения.
====================================
Ответ: [0; 1,5); 3; (3,5; 4) Автор: Ольга Себедаш Просмотров: 5400
|
