|
б) Круглая мишень разбита на 20 секторов, которые нумеруются по кругу
в каком‐либо порядке числами 1, 2, ..., 20. Если секторы занумерованы, например, в следующем порядке 1, 20, 5, 12, 9, 14, 11, 8, 16, 7, 19,
3, 17, 2, 15, 10, 6, 13, 4, 18, то наименьшая из разностей между
номерами соседних (по кругу) секторов равна 12 – 9 = 3. Может ли
указанная величина при нумерации в другом порядке быть больше 3?
в) Каково наибольшее возможное значение этой величины?
Задача расстановки чисел по кругу состоит в том, чтобы даже маленькие
промежутки между соседними числами были как можно больше. Какими?
Заметим, что не всё нам доступно. Можно ли сделать так, чтобы
наименьшее расстояние между соседями было равно, например 10?
Невозможно. Нет у числа 10 двух таких соседей. Есть один - 20.
То же самое можно сказать и о числе 11. У него один сосед - 1.
Если нам удастся расставить числа так, чтобы наибольшая дыра
между соседними была равна 9, то дело в шляпе. Задача решена.
Как примерно можно рассуждать? Возьмём кучку маленьких чисел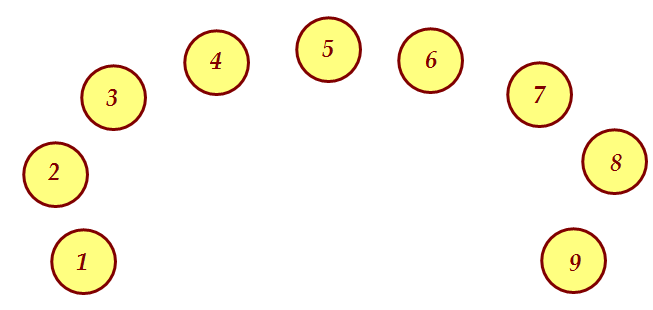
Никакие два из них соседями быть не могут, даже 9 - 1 < 9.
Значит, между ними надо вставлять большие числа. Как?
Попробуем первую приходящую в голову комбинацию
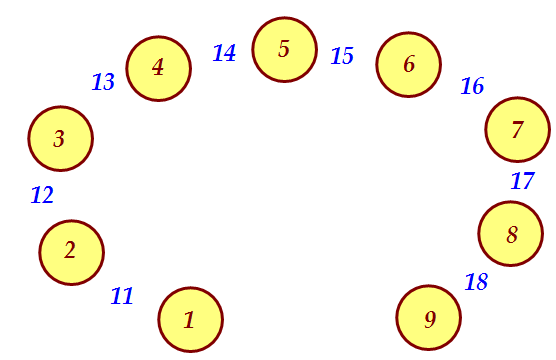Последние три числа приставим к полученным
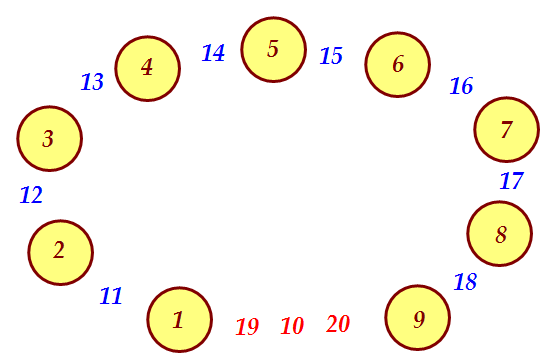Условие выполнено. Наибольшее расстояние равно 9.
Автор: Ольга Себедаш Просмотров: 4747
|
