|
15(C3). Логарифмическое неравенство с длииинным условием (вар. 149)
|
Решите неравенство
}}\cdot{log_{4x^2+28x+49}{(2-x)}}+log_{\frac{1}{x+4}}{x^2-5x+6}}\geq{0}) Для начала разложим квадратные трёхчлены на множители: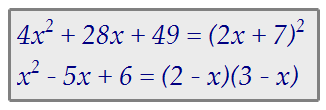
Заметьте, что второй квадратный трёхчлен разложен именно так. Почему?
Дело в том, что выражение (2 - х) стоит одиноко под вторым логарифмом.
Значит, 2 - х > 0, то есть x < 2. Из этого следует, что х < 3 и 3 - х > 0.Мы сможем на области определения легко "разорвать" третий логарифм.Найдём область допустимых значений данного неравенства:
1) 2x + 7 > 0, x + 4 > 0. Отсюда следует, что х > -3,5.
2) 2 - х > 0, x2 - 5x + 6 > 0. Отсюда следует, что x < 2.
3) x + 4 ≠ 1, 2x + 7 ≠ 1. Отсюда следует, что x ≠ -3.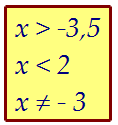 Ну а теперь по действиям на ОДЗ упростим левую часть неравенства:
}}\cdot{log_{4x^2+28x+49}{(2-x)}}={log_{x+4}{(2x+7)}}\cdot{log_{2x+7}{(2-x)}}=)
}{lg(x+4)}}\cdot{\frac{lg(2-x)}{lg(2x+7)}}=\frac{lg(2-x)}{lg(x+4)}=log_{x+4}{(2-x)})
}+log_{\frac{1}{x+4}}{(x^2-5x+6)}=log_{x+4}{(2-x)}-log_{x+4}{(2-x)(3-x)}=)
}-log_{x+4}{(2-x)}-log_{x+4}{(3-x)}=-log_{x+4}{(3-x)}) На области определения исходное неравенство равносильна новому:
Решим его на той же области определения методом рационализации:
(x + 4 - 1)(3 - x - 1) ≤ 0
(x + 3)(2 - x) ≤ 0
Поделим неравенство на положительный множитель (2 - х):
(x + 3) ≤ 0
х ≤ -3
Учитывая область определения, получаем окончательный ответ.Ответ: (-3,5; -3) Автор: Ольга Себедаш Просмотров: 3704
|
|
