|
Все ребра правильной четырехугольной пирамиды FABCD с основанием ABCD
равны 7. Точки P, Q, R лежат на ребрах FA, AB и ВС соответственно,причем FP = BR = 4, AQ = 3.
а) Докажите, что плоскость PQR перпендикулярна ребру FD
б) Найдите расстояние от вершины D до плоскости PQR
Сначала обратим внимание на свойство правильной четырёхугольной пирамиды,
у которой боковые рёбра равны рёбрам основания. Её диагональное сечение...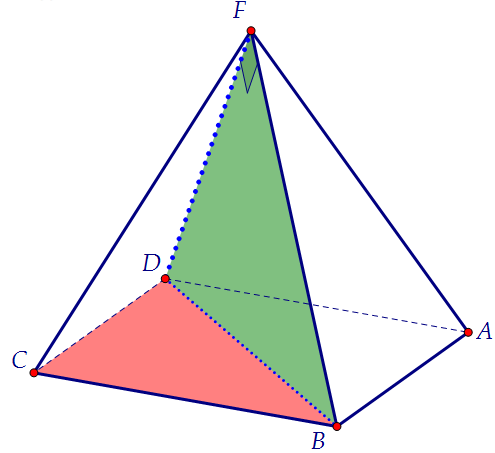 Верно! Это равнобедренный треугольник с прямым углом при вершине.
Всё дело в том, что треугольники DFB и CDB равны по трём сторонам.
Ну а теперь расставим данные точки и соединим Р и Q, R и Q.
Верно! Это равнобедренный треугольник с прямым углом при вершине.
Всё дело в том, что треугольники DFB и CDB равны по трём сторонам.
Ну а теперь расставим данные точки и соединим Р и Q, R и Q.
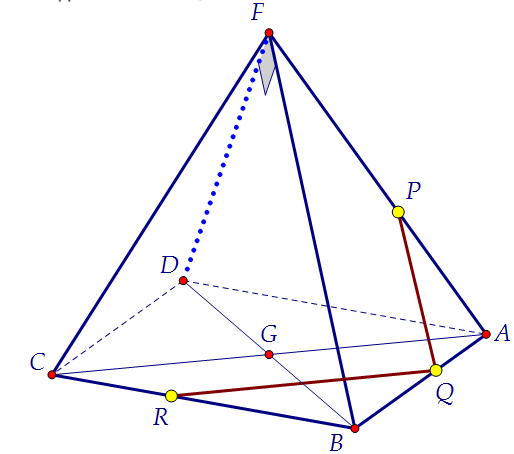 Для доказательства пункта а) сечение строить вовсе необязательно.
Достаточно доказать, что FD перпендикулярно двум пересекающимся
прямым плоскости PQR. Может, подойдут коричневые прямые PQ и QR?================================
1) Докажем, что FD перпендикулярно PQ.
Так как AQ : QB = AP : PF = 3 : 4, то PQ ∥ FB.
Так как DF ⊥ FB, то DF ⊥ PQ.================================
2) Докажем, что FD перпендикулярно RQ.
Так как BQ : QA = BR : RC = 4 : 3, то RQ ∥ AC.
DF ⊥ AC по теореме о трёх перпендикулярах.
Так как DF ⊥ АС, то DF ⊥ RQ.================================
Итак, DF перпендикулярна двум пересекающимся прямым плоскости PQR.
По признаку перпендикулярности прямой и плоскости DF ⊥ PQR, ч.т.д.================================
И для решения задачи б) можно сечение полностью не строить.
Искомым расстоянием является длина отрезка перпендикуляра,
опущенного из точки D на плоскость PQR, т.е. часть DF.
Нам важно найти точку пересечения отрезка DF и PQR.
Для доказательства пункта а) сечение строить вовсе необязательно.
Достаточно доказать, что FD перпендикулярно двум пересекающимся
прямым плоскости PQR. Может, подойдут коричневые прямые PQ и QR?================================
1) Докажем, что FD перпендикулярно PQ.
Так как AQ : QB = AP : PF = 3 : 4, то PQ ∥ FB.
Так как DF ⊥ FB, то DF ⊥ PQ.================================
2) Докажем, что FD перпендикулярно RQ.
Так как BQ : QA = BR : RC = 4 : 3, то RQ ∥ AC.
DF ⊥ AC по теореме о трёх перпендикулярах.
Так как DF ⊥ АС, то DF ⊥ RQ.================================
Итак, DF перпендикулярна двум пересекающимся прямым плоскости PQR.
По признаку перпендикулярности прямой и плоскости DF ⊥ PQR, ч.т.д.================================
И для решения задачи б) можно сечение полностью не строить.
Искомым расстоянием является длина отрезка перпендикуляра,
опущенного из точки D на плоскость PQR, т.е. часть DF.
Нам важно найти точку пересечения отрезка DF и PQR.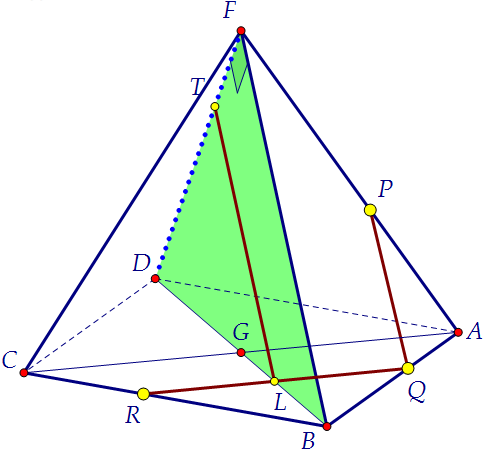 В плоскости диагонального сечения DFB через точку L проведём
прямую LT, параллельную прямой BF. Точка Т лежит на ребре FD.
Отрезок DT и есть искомый отрезок. Найдём его длину и решим б).
В плоскости диагонального сечения DFB через точку L проведём
прямую LT, параллельную прямой BF. Точка Т лежит на ребре FD.
Отрезок DT и есть искомый отрезок. Найдём его длину и решим б).
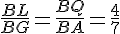
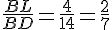
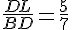
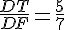
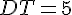 Ответ: 5 Ответ: 5
Автор: Ольга Себедаш Просмотров: 9931
|

 Верно! Это равнобедренный треугольник с прямым углом при вершине.
Всё дело в том, что треугольники DFB и CDB равны по трём сторонам.
Ну а теперь расставим данные точки и соединим Р и Q, R и Q.
Верно! Это равнобедренный треугольник с прямым углом при вершине.
Всё дело в том, что треугольники DFB и CDB равны по трём сторонам.
Ну а теперь расставим данные точки и соединим Р и Q, R и Q.
 Для доказательства пункта а) сечение строить вовсе необязательно.
Достаточно доказать, что FD перпендикулярно двум пересекающимся
прямым плоскости PQR. Может, подойдут коричневые прямые PQ и QR?================================
1) Докажем, что FD перпендикулярно PQ.
Так как AQ : QB = AP : PF = 3 : 4, то PQ ∥ FB.
Так как DF ⊥ FB, то DF ⊥ PQ.================================
2) Докажем, что FD перпендикулярно RQ.
Так как BQ : QA = BR : RC = 4 : 3, то RQ ∥ AC.
DF ⊥ AC по теореме о трёх перпендикулярах.
Так как DF ⊥ АС, то DF ⊥ RQ.================================
Итак, DF перпендикулярна двум пересекающимся прямым плоскости PQR.
По признаку перпендикулярности прямой и плоскости DF ⊥ PQR, ч.т.д.================================
И для решения задачи б) можно сечение полностью не строить.
Искомым расстоянием является длина отрезка перпендикуляра,
опущенного из точки D на плоскость PQR, т.е. часть DF.
Нам важно найти точку пересечения отрезка DF и PQR.
Для доказательства пункта а) сечение строить вовсе необязательно.
Достаточно доказать, что FD перпендикулярно двум пересекающимся
прямым плоскости PQR. Может, подойдут коричневые прямые PQ и QR?================================
1) Докажем, что FD перпендикулярно PQ.
Так как AQ : QB = AP : PF = 3 : 4, то PQ ∥ FB.
Так как DF ⊥ FB, то DF ⊥ PQ.================================
2) Докажем, что FD перпендикулярно RQ.
Так как BQ : QA = BR : RC = 4 : 3, то RQ ∥ AC.
DF ⊥ AC по теореме о трёх перпендикулярах.
Так как DF ⊥ АС, то DF ⊥ RQ.================================
Итак, DF перпендикулярна двум пересекающимся прямым плоскости PQR.
По признаку перпендикулярности прямой и плоскости DF ⊥ PQR, ч.т.д.================================
И для решения задачи б) можно сечение полностью не строить.
Искомым расстоянием является длина отрезка перпендикуляра,
опущенного из точки D на плоскость PQR, т.е. часть DF.
Нам важно найти точку пересечения отрезка DF и PQR. В плоскости диагонального сечения DFB через точку L проведём
прямую LT, параллельную прямой BF. Точка Т лежит на ребре FD.
Отрезок DT и есть искомый отрезок. Найдём его длину и решим б).
В плоскости диагонального сечения DFB через точку L проведём
прямую LT, параллельную прямой BF. Точка Т лежит на ребре FD.
Отрезок DT и есть искомый отрезок. Найдём его длину и решим б).