|
15(C3). Не потерять модуль в логарифмическом неравенстве (вар. 148)
|
Решите логарифмическое неравенство:
(x-5)}>log_{25}{(x-5)^2})
Приводя правый логарифм к основанию 5, важно не потерять модуль.
Иначе будет сужена область определения уравнения, так как (х - 5)
не обязано в первоначальном уравнении быть положительным.
(x-5)}>log_{5}{|x-5|})
Учитывая возрастание функции, переходим к следствию:
(x-5)>|x-5|)
Чтобы получить равносильную исходному неравенству систему,
потребуем лишь, чтобы |x - 5| > 0. Иначе говоря, х ≠ 5.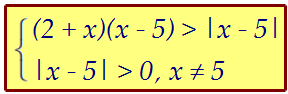
Решим неравенство с модулем при x < 5 и x > 5.============================
1) Если х < 5, то (2 + x)(x - 5) > -(х - 5)
Поделим обе части на отрицательное (х - 5):
2 + x < -1
x < -3
Учитывая, что х < 5 и х < -3, получим результат
============================
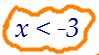2) Если х > 5, то (2 + x)(x - 5) > (х - 5)
Поделим обе части на положительное (х - 5):
2 + x > 1
x > -1
Учитывая, что х > 5 и х > -1, получим результат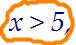
Ответ: (-∞; -3); (5; +∞) Автор: Ольга Себедаш Просмотров: 7948
|
|
