|
16(C4). Прямая, параллельная гипотенузе АВ треугольника АВС... (вар. 146)
|
Прямая, параллельная гипотенузе АВ прямоугольного треугольника АВС,
пересекает катет АС в точке D, катет ВС – в точке Е, причем DE = 2
и BE = 1. На гипотенузе взята точка F так, что BF = 1, а угол FCB
равен 30 градусов.
а) Докажите, что треугольник BFE равносторонний
б) Найдите площадь треугольника АВС. 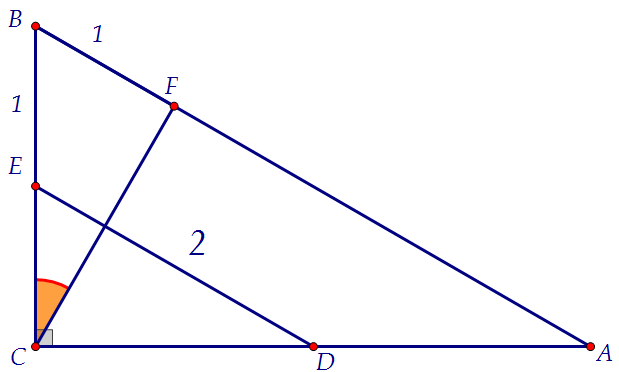 Идея номер один. Надо каким-то образом использовать, что 2 = 2·1.
Проведём FT ∥ ВС. ВFTЕ - параллелограмм по определению (даже ромб).
Идея номер один. Надо каким-то образом использовать, что 2 = 2·1.
Проведём FT ∥ ВС. ВFTЕ - параллелограмм по определению (даже ромб).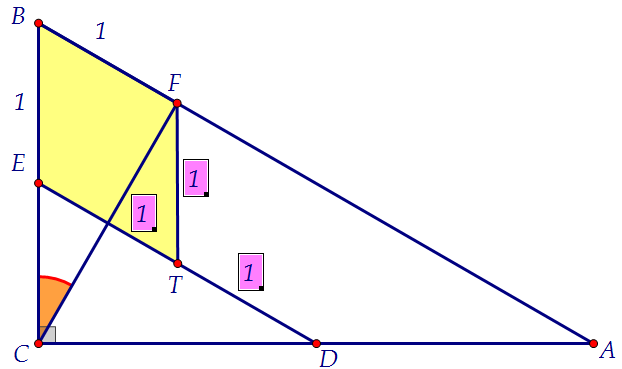 По свойству параллелограмма его противоположные стороны равны (по 1).
Идея номер два. В прямоугольном треугольнике CED точка Т вдруг оказалась
серединой гипотенузы. Значит, Т - центр описанной около CED окружности.
По свойству параллелограмма его противоположные стороны равны (по 1).
Идея номер два. В прямоугольном треугольнике CED точка Т вдруг оказалась
серединой гипотенузы. Значит, Т - центр описанной около CED окружности.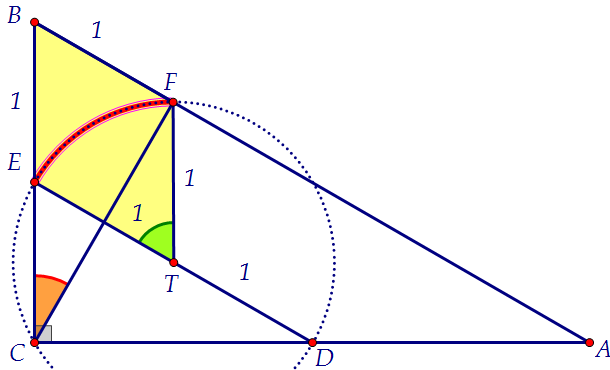 Данный угол 30° вписан в эту окружность, он опирается на красную дугу.
И значит, он в два раза меньше градусной меры этой самой красной дуги.
Центральный угол ETF равен градусной мере красной дуги, а значит, 60°.
Ну а в ромбе, понятное дело, противоположные углы равны. ∠В = 60°.
Треугольник BFE равносторонний (равнобедр. с углом при вершине 60°).
Площадь треугольника АВС ищется элементарно. Найдите её сами!
Данный угол 30° вписан в эту окружность, он опирается на красную дугу.
И значит, он в два раза меньше градусной меры этой самой красной дуги.
Центральный угол ETF равен градусной мере красной дуги, а значит, 60°.
Ну а в ромбе, понятное дело, противоположные углы равны. ∠В = 60°.
Треугольник BFE равносторонний (равнобедр. с углом при вершине 60°).
Площадь треугольника АВС ищется элементарно. Найдите её сами! Автор: Ольга Себедаш Просмотров: 8468
|
|

 Идея номер один. Надо каким-то образом использовать, что 2 = 2·1.
Проведём FT ∥ ВС. ВFTЕ - параллелограмм по определению (даже ромб).
Идея номер один. Надо каким-то образом использовать, что 2 = 2·1.
Проведём FT ∥ ВС. ВFTЕ - параллелограмм по определению (даже ромб). По свойству параллелограмма его противоположные стороны равны (по 1).
Идея номер два. В прямоугольном треугольнике CED точка Т вдруг оказалась
серединой гипотенузы. Значит, Т - центр описанной около CED окружности.
По свойству параллелограмма его противоположные стороны равны (по 1).
Идея номер два. В прямоугольном треугольнике CED точка Т вдруг оказалась
серединой гипотенузы. Значит, Т - центр описанной около CED окружности. Данный угол 30° вписан в эту окружность, он опирается на красную дугу.
И значит, он в два раза меньше градусной меры этой самой красной дуги.
Центральный угол ETF равен градусной мере красной дуги, а значит, 60°.
Ну а в ромбе, понятное дело, противоположные углы равны. ∠В = 60°.
Треугольник BFE равносторонний (равнобедр. с углом при вершине 60°).
Площадь треугольника АВС ищется элементарно. Найдите её сами!
Данный угол 30° вписан в эту окружность, он опирается на красную дугу.
И значит, он в два раза меньше градусной меры этой самой красной дуги.
Центральный угол ETF равен градусной мере красной дуги, а значит, 60°.
Ну а в ромбе, понятное дело, противоположные углы равны. ∠В = 60°.
Треугольник BFE равносторонний (равнобедр. с углом при вершине 60°).
Площадь треугольника АВС ищется элементарно. Найдите её сами!