Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найдите все значения а, при которых множество решений неравенства

|x - a| + |x + 3a| ≥ x² + a² содержит ровно четыре целых значения.

Есть замечательный способ решения неравенства |f(x)| ≥ g(x)



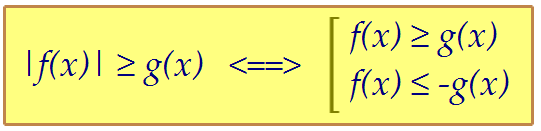Знаете ли Вы эту чудесную равносильность? Понимаете ли, что она верна
как для положительной, так и НЕ для положительной правой части?

Запишем исходное неравенство по-другому и решим его именно так:

|x - a| ≥ x² + a² - |x + 3a|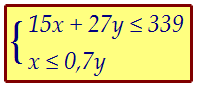









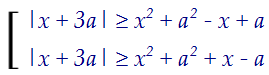
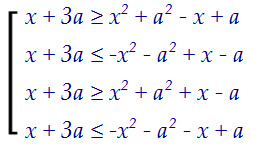
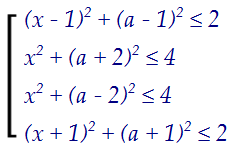Ну а теперь построим четыре круга и объединим их:



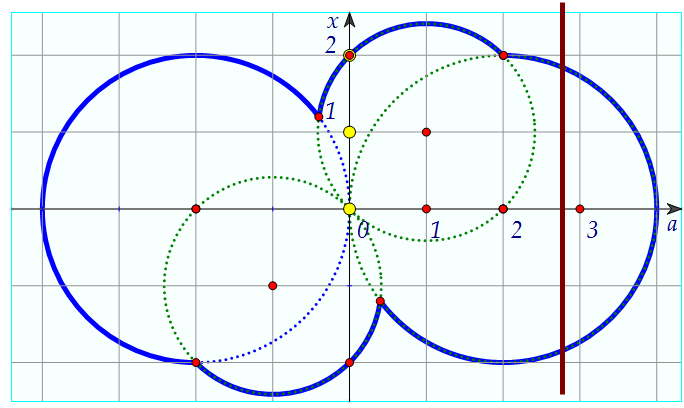Заметим, что круги симметричны относительно начала координат.
Кстати. Если (х, а) - решение неравенства, то и (-х, -а) - тоже.

Ну и на сцене появляется прямая, которая двигается вдоль оси а.

Следим, при каких значениях а выполняется условие задачи.

Ответ: (-2; 0); (0; 2)

Автор: Ольга Себедаш             Просмотров: 3871