|
14 а). В кубе точка N – середина ребра ВС, точка М лежит на ребре АВ (вар. 143)
|
В кубе АВСDA1B1C1D1 точка N – середина ребра ВС, точка М лежит на ребре АВ так,
что МВ = 2·МА. Плоскость, проходящая через точки М и N параллельно прямой ВD1, пересекает ребро DD1 в точке К.
а) Докажите, что DK : D1K = 5 : 2.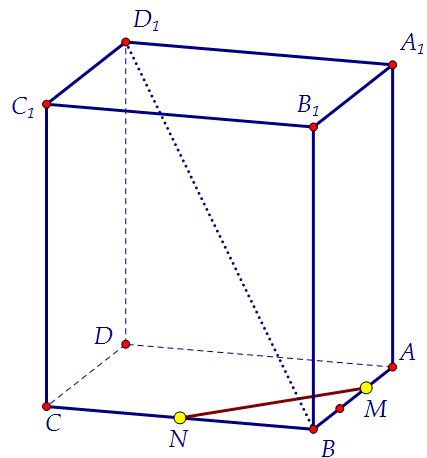
Чтобы провести плоскость через отрезок MN параллельно диагонали куба,
надо зацепиться за какую-нибудь точку отрезка MN и провести через неё
прямую, параллельную данной диагонали. За какую точку зацепиться?
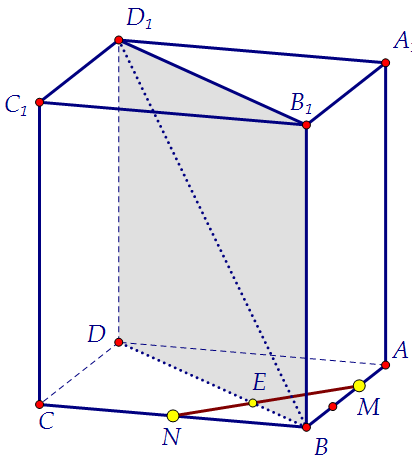В диагональной серой плоскости лежит и данная диагональ куба, и точка Е.Вот за эту точку Е и зацепимся и проведём через неё в серой плоскости
прямую ЕК || BD1. Заметьте! Сечение строить вовсе и необязательно!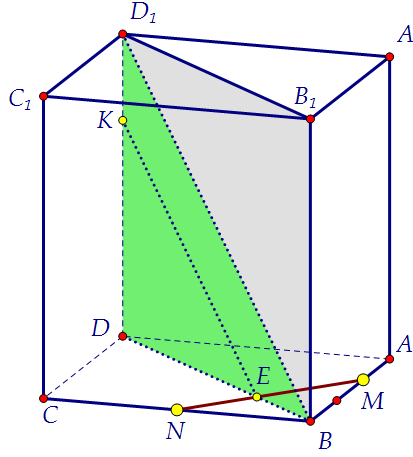
Плоскость сечения (пока не построенного) параллельна прямой BD1по признаку параллельности прямой и плоскости. Найдём DK : D1K.
Воспользуемся теоремой Фалеса в треугольнике DD1B
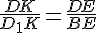Поиском последнего отношения и займёмся в обыкновенном квадрате АВСD.
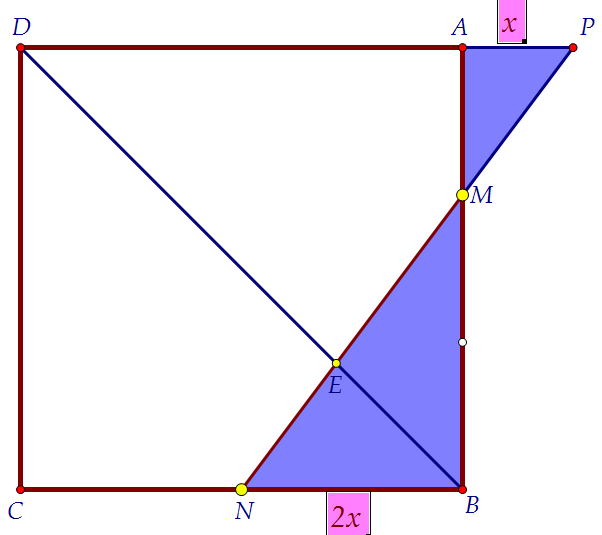Продлим MN до пересечения с DA в точке Р. Увидим подобные треугольники.
Коэффициент подобия очевиден и равен 2. Очевидно также, что AD = 4x.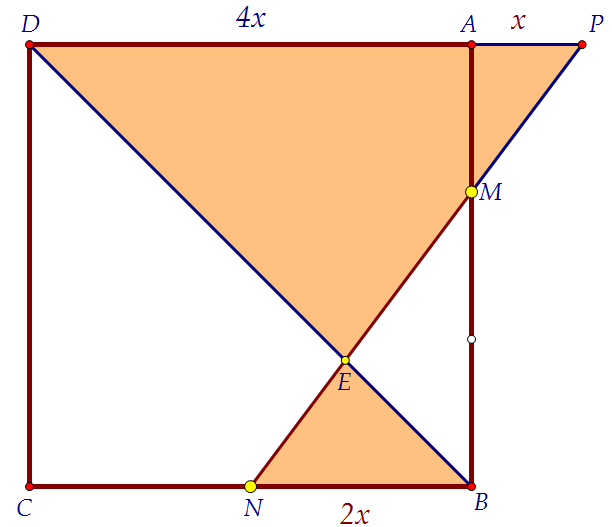
Рассмотрим ещё одну пару подобных треугольников. Коэффициент их подобия 2,5.
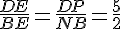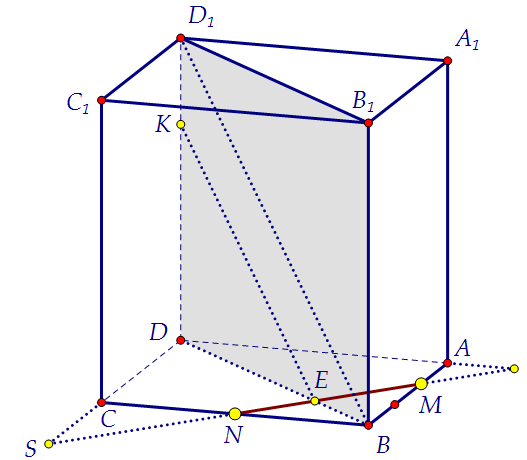Почему бы теперь не достроить и само сечение?  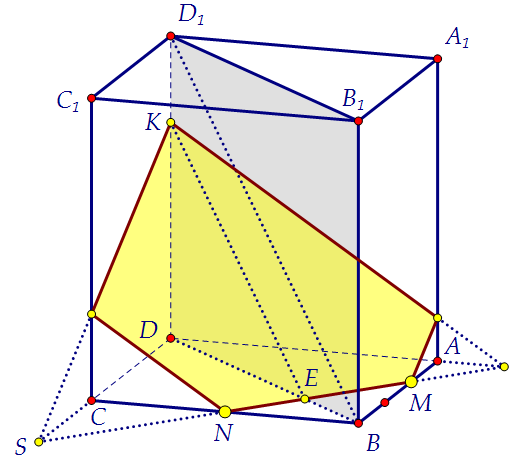Автор: Ольга Себедаш Просмотров: 8154
|
|
