Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Саша положил некоторую сумму в банк на 4 года под 10% годовых. Одновременно
с ним Паша такую же сумму положил на два года в другой банк под 15% годовых.
Через два года Паша решил продлить срок вклада еще на 2 года. Однако к тому времени
процентная ставка по вкладам в этом банке изменилась и составляла уже p% годовых.
В итоге через четыре года на счету у Паши оказалась большая сумма, чем у Саши, причем
эта разность составила менее 10% от суммы, вложенной каждым первоначально.
Найдите наибольшее возможное целое значение процентной ставки р.

Все четыре года вклад Саши возрастал в 1,1 раза и стал он в итоге 1,1⁴х руб.
Первые два года вклад Паши возрастал в 1,15 раза, а следующие два года?
Пусть дальше он возрастал в а раз. И стал он в итоге 1,15²·a²x руб.

Т.к. в результате разность вкладов оказалась меньше, чем 0,1х, то





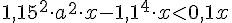
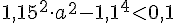Вы можете решить это неравенство, не используя калькулятор? Я не могу))
Поэтому упростим и будем решать честным обоснованным подбором.





Какой может быть новая процентная ставка у Паши? Допустим, 10%, т.е. а = 1,1.
Посчитаем устно: 115·1,1 = 115 + 11,5 = 126,5. Подставим:



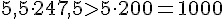Значит, новая процентная ставка меньше 10%, пусть она равна 9%, т.е. а = 1,09.
Посчитаем устно: 115·1,09 = 115 + 10,35 = 125,35. Подставим:



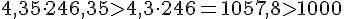Значит, новая процентная ставка меньше 9%, пусть она равна 8%, т.е. а = 1,08.
Посчитаем устно: 115·1,08 = 115 + 9,2 = 124,2. Подставим:



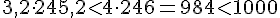Ура! Ответ получен! Новая Пашина процентная ставка 8%.

Автор: Ольга Себедаш             Просмотров: 14782