Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В окружности проведены хорды АС и ВD, пересекающиеся в точке О, причем
касательная к окружности, проходящая через точку С, параллельна ВD.
а) Докажите, что DС² = АС ∙ СО.
б) Найдите площадь треугольника СDО, если известно, что АВ : ВО = 3 : 1,
а площадь треугольника АСD равна 36.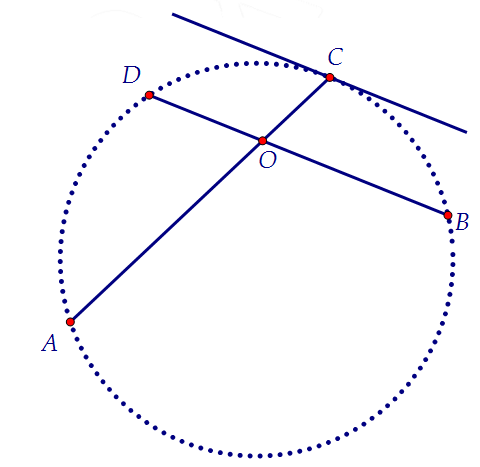



Равенство, которое требуется доказать, можно записать иначе:



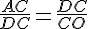Чтобы доказать пропорцию, надо найти на рисунке подобные треугольники.
Слева отношение двух сторон треугольника ADC, справа - треугольника DOC.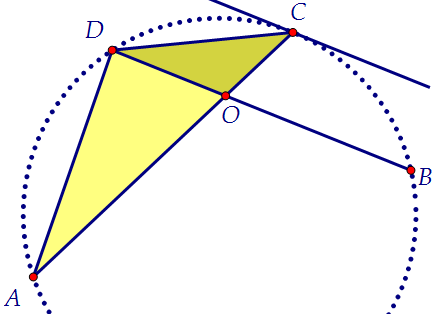



Итак, эти треугольники подобны. Почему? Один угол (∠ С) у них общий.



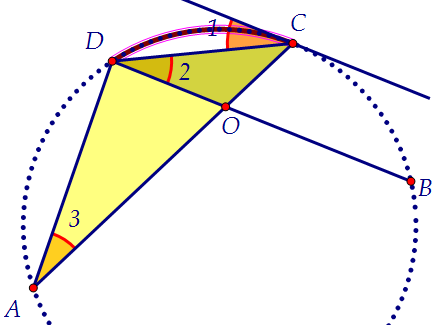∠1 = ∠2 как внутренние накрест лежащие при параллельных прямых и секущей.
∠1 = ∠3. ∠1 - это угол между хордой и касательной, а ∠3 - вписанный угол.
Оба они равны половине дуги DC, а значит, равны друг другу.
Значит, ∠2 = ∠3, и значит, треугольники ADC и DOC подобны.
Таким образом, верна пропорция, ч.т.д.



Для решения пункта б) призовём на помощь третий треугольник АОВ:



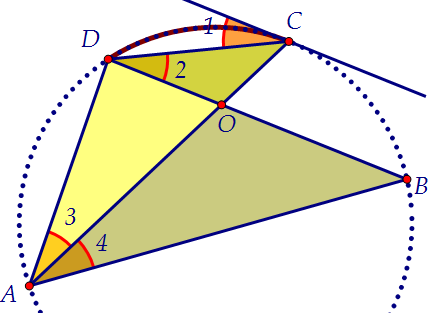Треугольники АОВ и DOC, подобны, т.к. ∠3 = ∠4 (опираются на одну дугу)
и углы при вершине О равны как вертикальные. По условию АВ : ВО = 3 : 1.



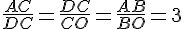Снова вернёмся к первым двум подобным треугольникам ADC и DOC
Посмотрите на равенство иначе - найден коэффициент подобия k.



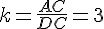Линейные размеры подобных треугольников отличаются в три раза.
Значит, их площади отличаются в 3² = 9 раз.
Площадь треугольника АСD равна 36.
Площадь треугольника СDО равна 4.

Автор: Ольга Себедаш             Просмотров: 7235