|
16(C4). В ромб вписана окружность (вар. 141)
|
В ромб вписана окружность Θ. Окружности w1 и w2 (разного радиуса) расположены
так, что каждая касается окружности Θ и двух соседних сторон ромба.
б) Найдите отношение радиусов окружностей w1 и w2, если известно,что диагонали ромба относятся, как 1 : 2.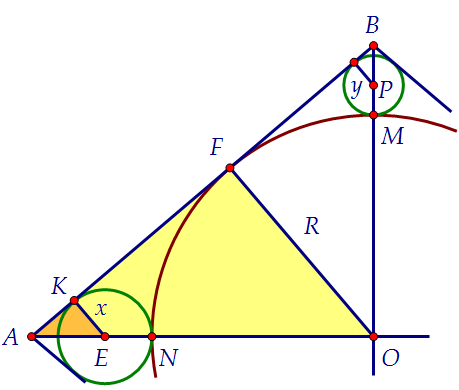
Из центров всех трёх окружностей проведём перпендикуляры к стороне ромба.
План наших действий таков:
1) Приняв половины диагоналей ромба за 1 и 2, найдём R.
2) Из подобия треугольников АКЕ и AFO выразим х через R.
3) Из аналогичной пары треугольников, выразим y через R.
4) Найдём отношение x к y. Задача будет решена.
Поехали...
1) Если ОВ = 1 и ОА = 2, то АВ = √5. Т.к. 1·2 = R·√5, то
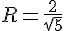2) Так как ОЕ = R + x, то АЕ = 2 - R - x. Составим пропорцию:
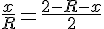
=\frac{2-R}{2})
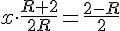
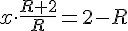
}{2+R})
3) Так как OP = R + y, то BM = 1 - R - y. Составим пропорцию:
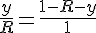
=1-R)
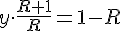
}{1+R})
3) Ну и поделим х на y:
(1+R)}{(2+R)(1-R)})
Подставив в отношение найденное R, получим:
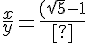(\sqrt{5}+2)}{(\sqrt{5}+1)(\sqrt{5}-2)}=\frac{7+3\sqrt{5}}{2}) Автор: Ольга Себедаш Просмотров: 6767
|
|
