Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

в) В клетках таблицы 3х3 расставлены девять различных натуральных чисел.
Рассмотрим восемь произведений: произведения трёх чисел в каждой строке,
каждом столбце и по двум диагоналям. Могут ли все эти произведения
оказаться одинаковыми? 

Поставим в середину таблички число 1. И заполним как-то первую строчку:



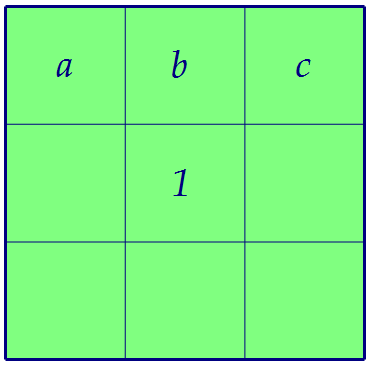Пусть каждое произведение равно, например, k. Заполним третью строку:



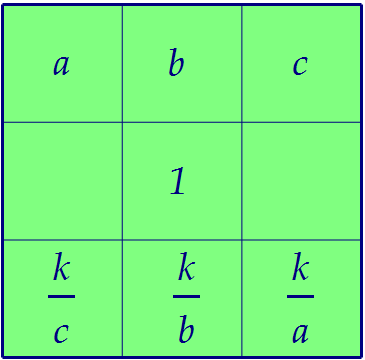В оставшиеся две клетки тоже легко вставить подходящие числа:



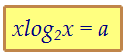Произведение чисел во второй строке оказалось равным 1, т.е. k = 1.
Окончательная табличка сформировалась. Но она пока дробная: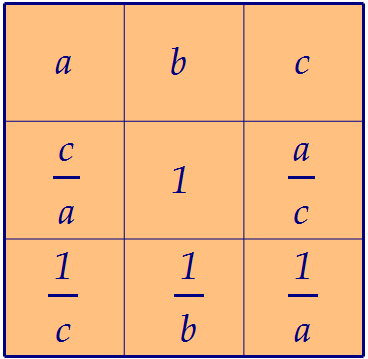



Подберём три числа a, b и с, произведение которых равно единице:



Заполним табличку сначала дробными числами, затем каждое умножим на 12:



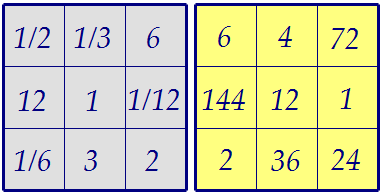Подберём новые числа a, b и с, произведение которых равно единице:



Заполним табличку сначала дробными числами, затем каждое умножим на 10:





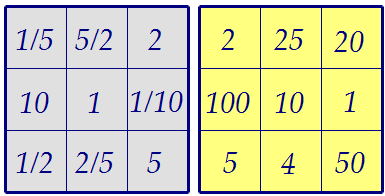Возможна другая стратегия. Нам поможет классический магический квадрат.
Все восемь сумм этого квадрата равны 15, все девять чисел различны.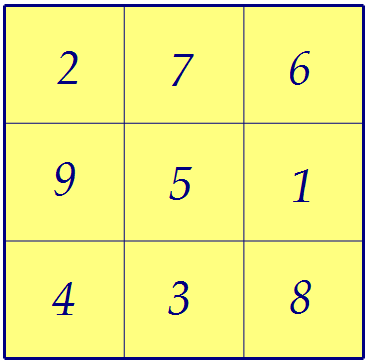



Превратим эти числа в показатели любого натурального числа (например, 3):



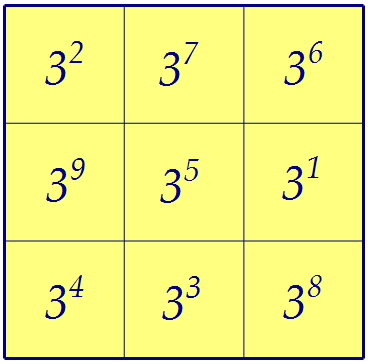Условие задачи при этом будет выполнено.

Автор: Ольга Себедаш             Просмотров: 13706