Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

16(C4). Из точки на окружности на диаметры опущены перпендикуляры МК и МР (вар. 140)

Из точки М, взятой на окружности с центром в точке О, на диаметры АВ и СD
опущены перпендикуляры МК и МР соответственно.
а) Докажите, что существует точка, одинаково удалённая от точек М, О, Р, К.
б) Найдите площадь треугольника МКР, если известно,
что ∠МКР = 30°, ∠АОС = 15°, а радиус окружности равен 4.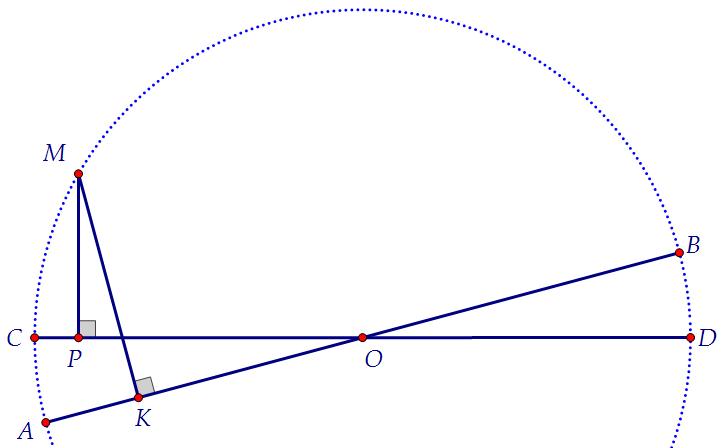

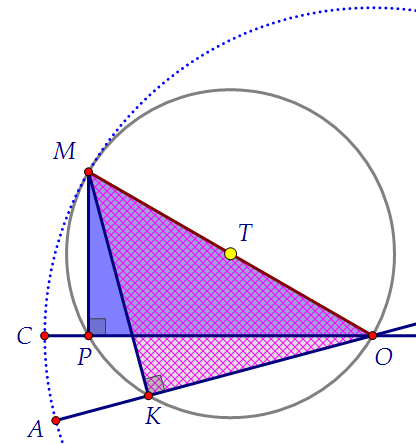Из точки на окружности на диаметры опущены перпендикуляры МК и МР (вар. 140)

Не спешите сдаваться. Посмотрите на чертёж. Где искомая точка?
Та самая, которая одинаково удалена от М, О, Р и К. Где же?
Правильно, это середина ОМ. Почему? Объясните сами.

Из точки на окружности на диаметры опущены перпендикуляры МК и МР (вар. 140)

Теперь изобразим на чертеже данные в условии углы:

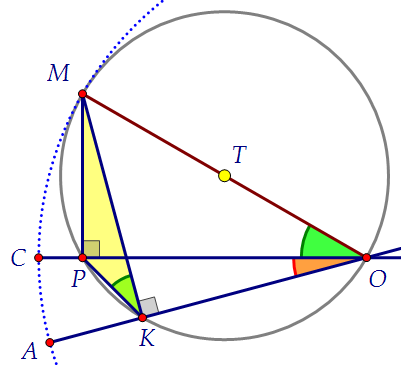16(C4). Из точки на окружности на диаметры опущены перпендикуляры МК и МР (вар. 140)

Красным закрашен угол 15°, зелёным - угол 30°. Почему же их два?
Потому что они опираются на одну и туже дугу МР, и значит, равны.

В жёлтом треугольнике известны все три угла: 15°, 135° и 30°.
Можем ли мы узнать все стороны? Проще всего найти МР и МК.

МР = 2 найдём из синего прямоугольного треугольника с углами 30° и 60°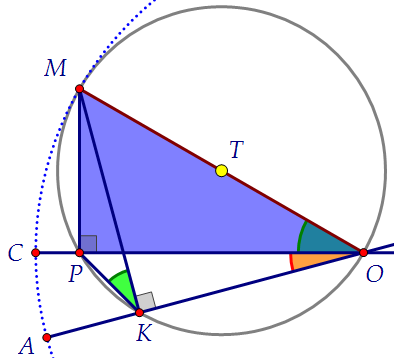

16(C4). Из точки на окружности на диаметры опущены перпендикуляры МК и МР (вар. 140)

МК = 2√2 найдём из зелёного равнобедр. прямоугольного треугольника:

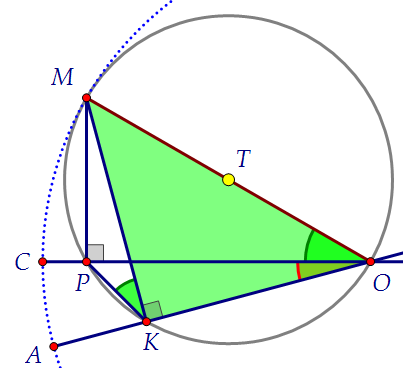Между найденными сторонами в искомом треугольнике находится угол 15°.

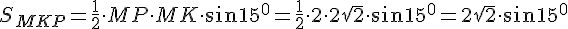$S_{MKP}=\frac{1}{2}\cdot{MP}\cdot{MK}\cdot{sin15^0}=\frac{1}{2}\cdot{2}\cdot{2\sqrt{2}}\cdot{sin15^0}={2\sqrt{2}}\cdot{sin15^0}$

Займёмся углом 15°. Как вычислить его синус? Например, так:

$sin{15^0}=sin(45^0-30^0)={sin45^0}\cdot{cos30^0}-{cos45^0}\cdot{sin30^0}$

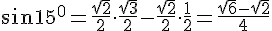$sin{15^0}={\frac{\sqrt{2}}{2}}\cdot{\frac{\sqrt{3}}{2}}-{\frac{\sqrt{2}}{2}}\cdot{\frac{1}{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}$

Вернёмся к вычислению площади треугольника МКР:

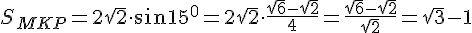$S_{MKP}={2\sqrt{2}}\cdot{sin15^0}={2\sqrt{2}}\cdot{\frac{\sqrt{6}-\sqrt{2}}{4}}=\frac{\sqrt{6}-\sqrt{2}}{\sqrt{2}}=\sqrt{3}-1$

Автор: Ольга Себедаш Просмотров: 5604

Постоянно работают курсы для выпускников, учителей и репетиторов

Комментарии к этой задаче:

Комментарий добавил(а): Алексей
Дата: 2016-03-15

Если абитуриент оставит в ответе "sin 15", будет ли этот ответ правильным?

Добавить Ваш комментарий:

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников

Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников