Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
14(C2). В правильной четырехугольной пирамиде РАВСD высота в полтора раза ... (вар. 140)
Комментарии к этой задаче: Комментарий добавил(а): 3aplus63drads <b></b> Комментарий добавил(а): 3aplus63drads <b></b> Добавить Ваш комментарий: |

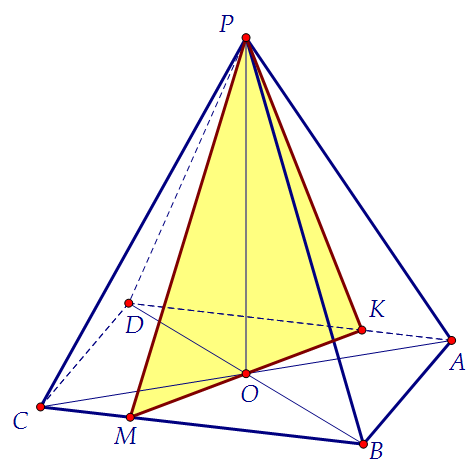 Возьмём точку М на стороне ВС основания пирамиды и проведём луч МО
до пересечения со стороной АD в точке К. Найдём длину отрезка МК.
Возьмём точку М на стороне ВС основания пирамиды и проведём луч МО
до пересечения со стороной АD в точке К. Найдём длину отрезка МК.
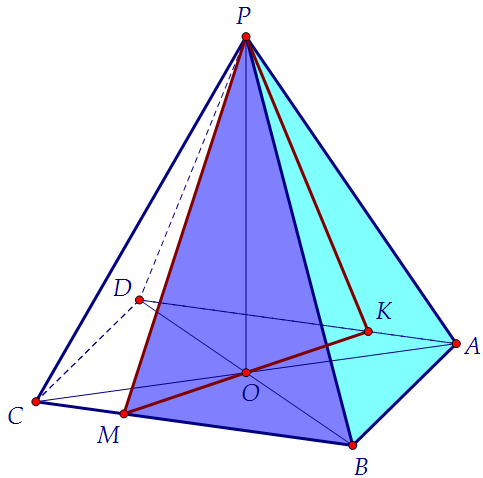 - из площади её основания АКМВ (половина площади квадрата);
- из площади сечения РКМ (по условию равна площади квадрата);
- из суммы площадей граней РМВ и РАК (а это площадь СРВ);
- из площади грани АРВ (тоже просто боковая грань).
- из площади её основания АКМВ (половина площади квадрата);
- из площади сечения РКМ (по условию равна площади квадрата);
- из суммы площадей граней РМВ и РАК (а это площадь СРВ);
- из площади грани АРВ (тоже просто боковая грань).