Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В остроугольном неравнобедренном треугольнике АВС проведены высоты
АА₁ и СС₁. Точки А₂ и С₂ симметричны середине стороны АС относительно
прямых ВС и АВ соответственно.
а) Докажите, что отрезки А₁А₂ и С₁С₂ лежат на параллельных прямых. 
б) Найдите расстояние между А₂ и С₂, если известно, что АВ=7, ВС=6, СА=5.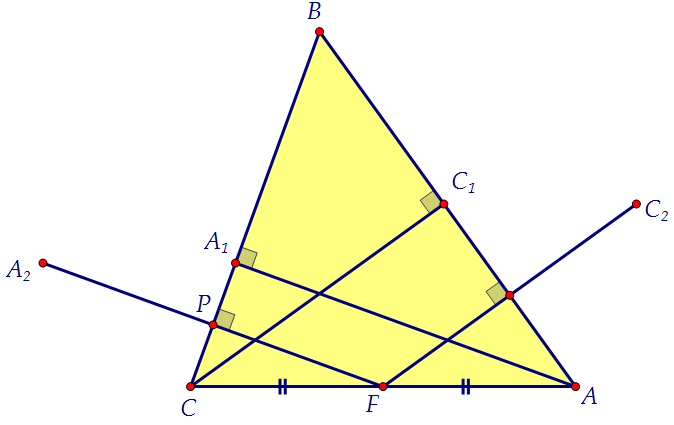



Докажем сначала, что четырёхугольник А₁А₂СF является параллелограммом.



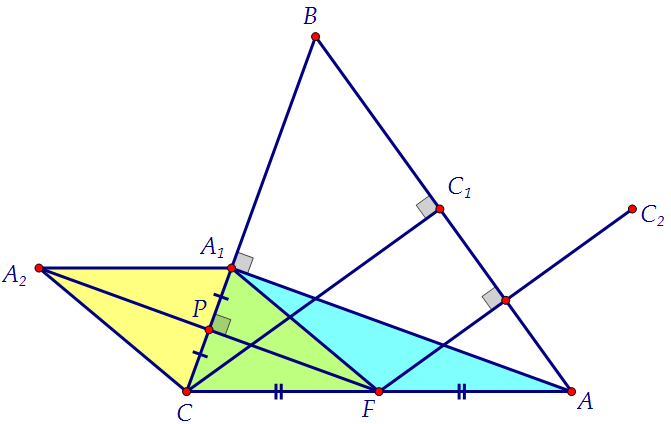1) FP ⊥ BC по определению осевой симметрии, АА₁ ⊥ ВС по условию.
Две прямые, перпендикулярные третьей, параллельны. FP || AA₁.

2) По т. Фалеса точка Р поделит СА₁ пополам. СР = РА₁.

3) FР = РА₂ по определению осевой симметрии.

Итак, в четырёхугольнике А₁А₂СF диагонали пересекаются и в точке
пересечения делятся пополам. Значит, А₁А₂СF - параллелограмм.

По определению параллелограмма А₂А₁ || CF. Аналогично С₂С₁ || AF.
Две прямые, параллельные третьей, параллельны, А₂А₁ || С₂С₁, ч.т.д.
(факт, что четырёхугольник А₁А₂СF является ромбом, нам НЕ нужен)



Чтобы найти длину А₂С₂, применим теорему косинусов в треугольнике А₂FС₂:



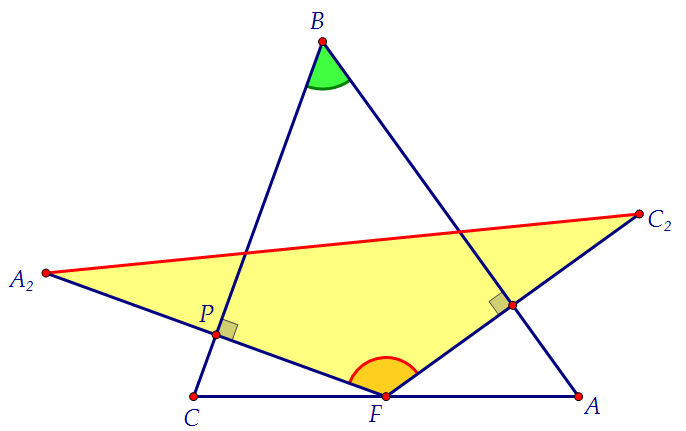Для этого нам понадобятся длины сторон FA₂ и FC₂ и косинус угла A₂FC₂.
Косинус угла F противоположен косинусу угла В (сумма углов равна 180°).
А стороны FA₂ и FC₂ равны высотам треугольника АВС. Покажем это.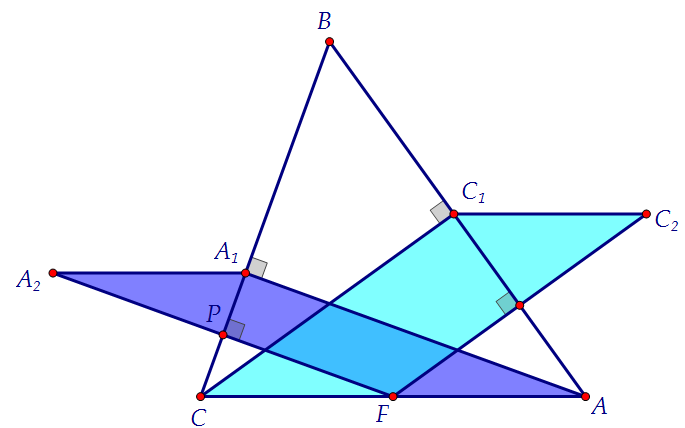



Т.к. А₁А₂СF параллелограмм, то А₁А₂ = СF. Но CF = FA. Следовательно, А₁А₂ = АF.
Т.к. А₁А₂ = АF и А₁А₂ || АF, то А₂А₁АF - параллелограмм по признаку пар-мма.
Значит, FА₂ = AА₁ по свойству параллелограмма. Аналогично, FС₂ = СС₁.

Чтобы найти высоты треугольника, найдём его площадь по формуле Герона.









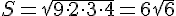
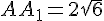
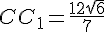Мы знаем высоты треугольника АВС, а значит, стороны треугольника FA₂C₂.

По теореме косинусов в треугольнике АВС найдём косинус угла В:







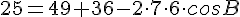
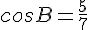
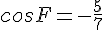Осталось применить теорему косинусов в треугольнике А₂FС₂:

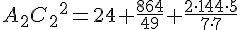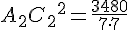
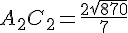Автор: Ольга Себедаш             Просмотров: 5755