|
а) Найдите наим. натуральное число такое, что оно не является делителем 100!
б) Определите, на какую наибольшую степень 10 делится 100!
в) Найдите последнюю ненулевую цифру в записи числа, равного 100!
а) 100! = 1·2·3·4·5·6·7·8·9·10·11·12·...·89·90·91·92·93·94·95·96·97·98·99·100
Число 100! делится на все числа до ста, включая и 100. Число 101 является простым и не входит в состав множителей числа 100! 101 и есть ответ на а).
Заметьте! Если исходным было бы число 200!, то ответом было бы не 201.
б) Чтобы посчитать число нулей, на которые заканчивается запись числа 100!,
достаточно посчитать количество пятёрок в разложении 100! на множители.
На каждую пятёрку найдётся своя двойка. Каждая такая пара и даст ноль.Как посчитать пятёрки? Заметим, что каждое пятое число делится на пять.
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.
Но кроме того, в первой сотне есть четыре числа, которые делятся на 25:
25, 50, 75, 100. Иначе говоря, эти числа включают в себя две пятёрки.
Таким образом, пятёрок в разложении 100! на множители 24 штуки.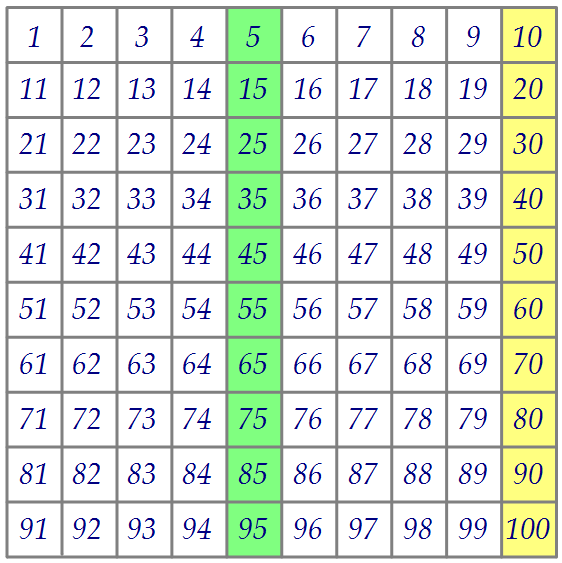
Заметим, что все пятёрки находятся в зелёном и жёлтом столбцах (по 12 штук).
В зелёном их 10+2 (в числах 25 и 75), в жёлтом их тоже 10+2 (50 и 100).
в) Чтобы найти посл. ненулевую цифру, уберём все 24 пятёрки и 24 двойки.
Пятёрки уберём разом, а двоек для начала 11 (11 нулей в жёлтом столбце).
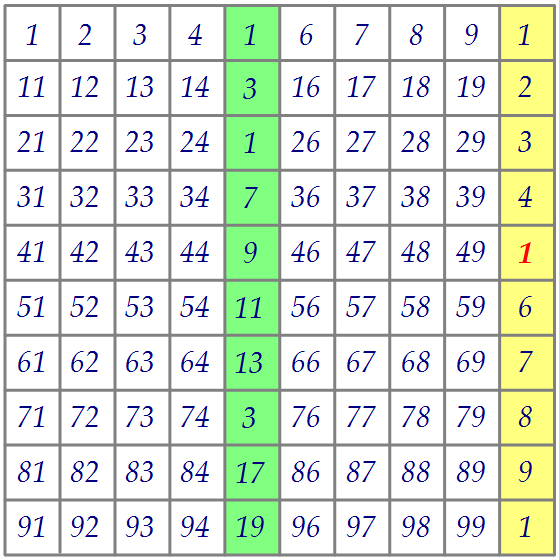Осталось убрать 24 - 11 = 13 двоек. Из последнего столбца уберём 7 двоек (числа 2, 4, 6, 8), а ещё шесть штук уберём из первой строки (числа 2, 4, 8). 
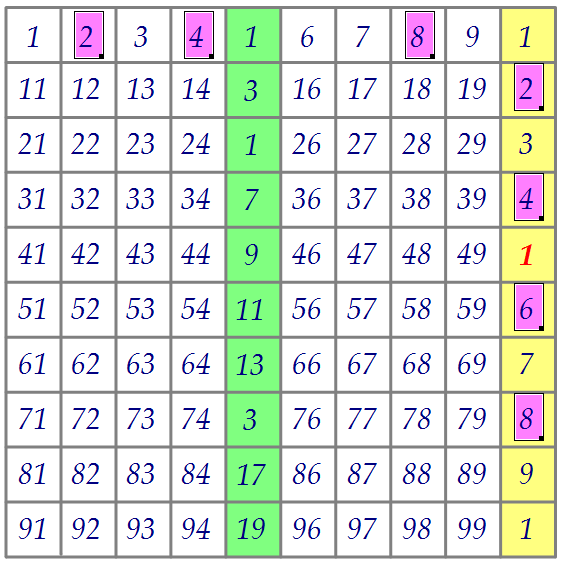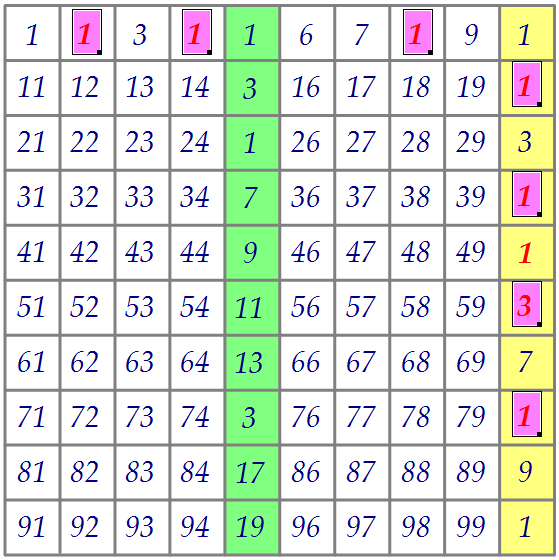Произведение оставшихся чисел в серой строке, заканчивается цифрой 6.
В каждой из девяти серых строк результат, разумеется, тот же. 6· 6= 36.Таким образом, произведение всех 72-ух серых чисел оканчивается на 6.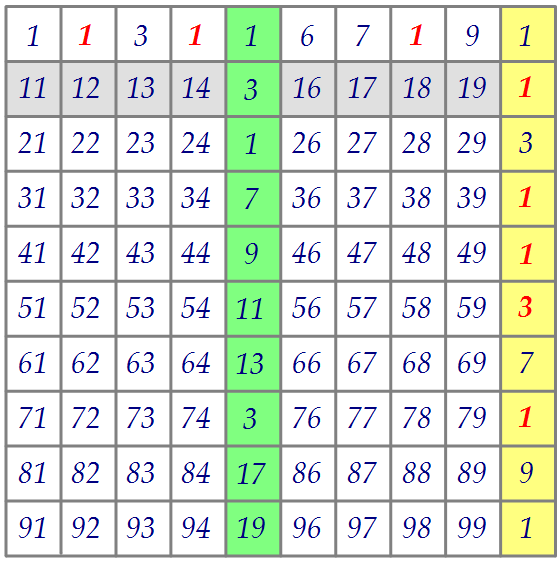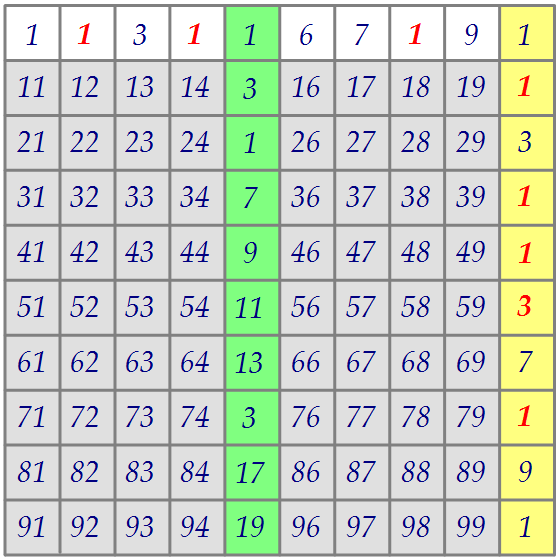 
Осталось перемножить числа, стоящие на белых, жёлтых и зелёных местах.
Замечаем, что произведения 3 и 17, а также 19 и 9, не говоря уже об 11 и 1,нас совершенно не интересуют, т.к. на результат не влияют.
Ответ: 101, 24, 4 Автор: Ольга Себедаш Просмотров: 8216
|
