|
18(C5). Найти все а, при которых система имеет ровно одно решение (вар. 136)
|
 ^2+x(y-5) & = & 0 \\
y=ax^2+2 \\
x \geq 2 \\
\end{array}
\right) (y-(5-x)) & = & 0 \\
y=ax^2+2 \\
x \geq 2 \\
\end{array}
\right) Графиком первого уравнения являются две коричневые прямые y = 5 и y = 5 - x.
Третье условие х ≥ 2 ограничивает правую (серую) полуплоскость с границей х = 2.
Графиком второго уравнения при а ≠ 0 является парабола, при а = 0 - прямая y = 2.Посмотрите на примеры поведения системы при положительном а:
Графиком первого уравнения являются две коричневые прямые y = 5 и y = 5 - x.
Третье условие х ≥ 2 ограничивает правую (серую) полуплоскость с границей х = 2.
Графиком второго уравнения при а ≠ 0 является парабола, при а = 0 - прямая y = 2.Посмотрите на примеры поведения системы при положительном а: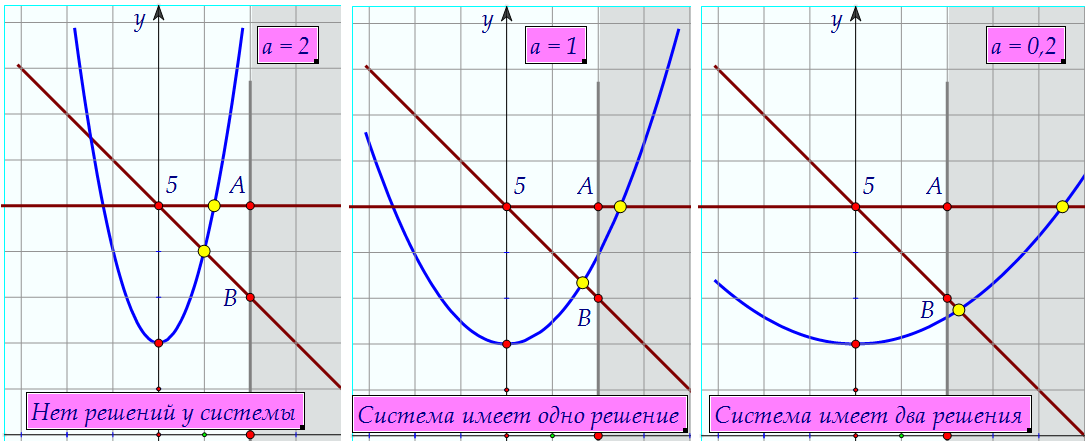 Посмотрите на примеры поведения системы при отрицательных а: Посмотрите на примеры поведения системы при отрицательных а: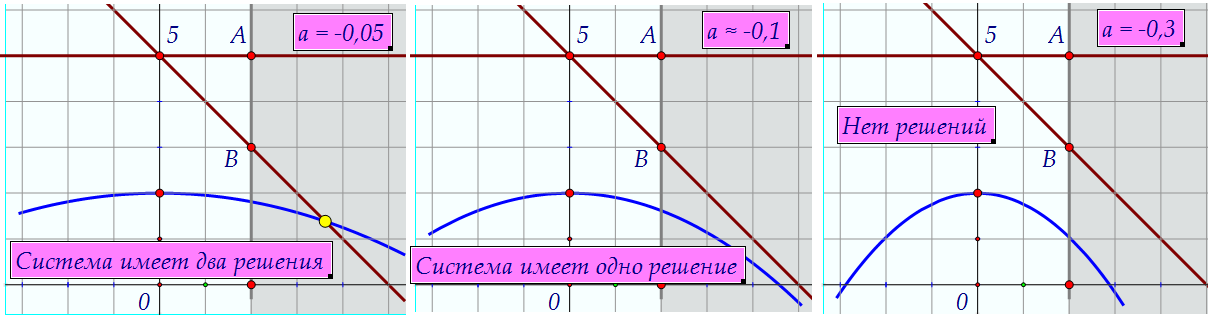 Для положительных а важны моменты прохождения параболы через точки А и В.
Для положительных а важны моменты прохождения параболы через точки А и В.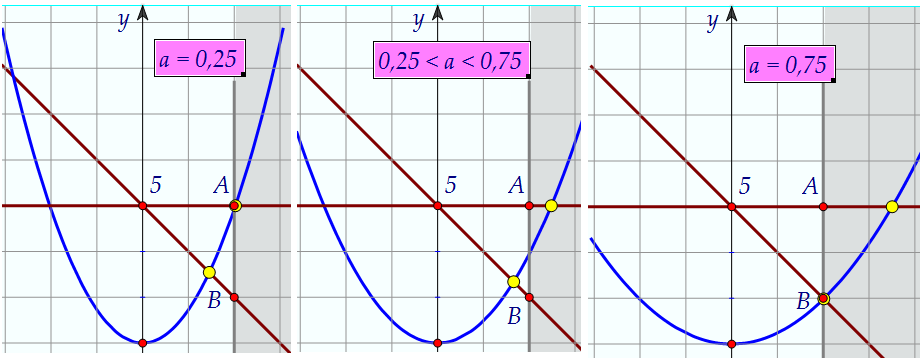 Как же найдены значения а на этих картинках? Элементарно!
Пусть парабола y = ax2 + 2 проходит через точку А(2, 5).
Как же найдены значения а на этих картинках? Элементарно!
Пусть парабола y = ax2 + 2 проходит через точку А(2, 5).
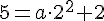
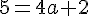
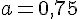 Пусть парабола y = ax2 + 2 проходит через точку B(2, 3).
Пусть парабола y = ax2 + 2 проходит через точку B(2, 3).
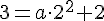
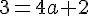
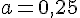 Из всех положительных а нас устраивает интервал (0,25; 0,75) и сама точка 0,75.
А из всех отрицательных а нас устроит лишь то, при котором происходит касание.Парабола и прямая y = 5 - x должны иметь одну общую точку. Иначе говоря,квадратное уравнение ax2 + 2 = 5 - х должно иметь единственное решение.
ax2 + x - 3 = 0
D = 1 + 12a = 0
Из всех положительных а нас устраивает интервал (0,25; 0,75) и сама точка 0,75.
А из всех отрицательных а нас устроит лишь то, при котором происходит касание.Парабола и прямая y = 5 - x должны иметь одну общую точку. Иначе говоря,квадратное уравнение ax2 + 2 = 5 - х должно иметь единственное решение.
ax2 + x - 3 = 0
D = 1 + 12a = 0
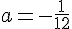 При а = 0 система имеет единственное решение (3; 2).
Ответ: 0, (0,25; 0,75],
При а = 0 система имеет единственное решение (3; 2).
Ответ: 0, (0,25; 0,75], 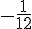
Автор: Ольга Себедаш Просмотров: 4534
|
|

