|
На проекте «Вышка» каждый прыжок в воду оценивают пять судей. При этом
каждый судья выставляет оценку – целое число баллов от 0 до 6 включительно.
Известно, что за прыжок Тимура Ласточкина все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за прыжок определялся как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются наименьшая и наибольшая оценки, и считается среднее арифметическое трех оставшихся оценок.
а) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 1/10?
б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 1/15?
В) Найдите наибольшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания.
Представим себе выставленные оценки нарисованными на пяти цветных шариках.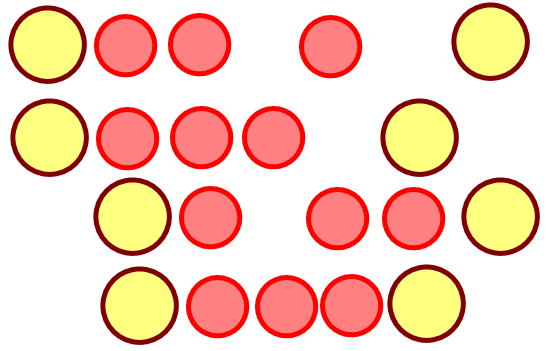
Крайние оценки могут быть такими: 0 и 6, 0 и 5, 0 и 4, 1 и 6, 1 и 5.
Средние красные шарики перекатываются между крайними жёлтыми.
Обозначим сумму крайних оценок буквой а, сумму средних - буквой b.
Найдём старую и новую оценки, используя среднее арифметическое:
 
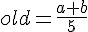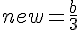Найдём их разность и посмотрим, какие она может принимать значения. =====================================
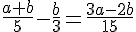Ответим на вопрос пункта а)
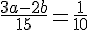
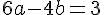В левой части уравнения - чётное число, в правой - нечётное. Значит, решений в целых числах уравнение не имеет. Ответ на пункт а) - нет.=====================================
Ответим на вопрос пункта б)
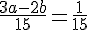
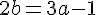Слева - чётное число, значит, и справа - чётное. Значит, а нечётное.Пусть a = 2k + 1. Тогда
-1)
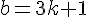При k = 2 получаем, что а = 5, b = 7. Это одно из решений уравнения.
При k = 3 получаем, что а = 6, b = 10. Это ещё одно решение уравнения. =====================================
Ответим на вопрос пункта в)
}\leq{\frac{2}{5}})
Искомая разность не может оказаться больше, чем 2/5. Но может ли она
быть равной 2/5? Если привести такой пример, то ответ на пункт в) готов.------------------------------
Чтобы это осуществить, сделаем сумму трёх красных шариков самой маленькой из возможных (1 + 2 + 3), а сумму жёлтых при этом - самой большой (0 + 6) }={\frac{2}{5}}\cdot{(\frac{6}{2}-\frac{6}{3})}={\frac{2}{5}}\cdot{(3-2)}=\frac{2}{5}) Автор: Ольга Себедаш Просмотров: 4997
|
