Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

16(C4). В треугольнике АВС проведена биссектриса СМ (вар. 116)

В треугольнике АВС проведена биссектриса СМ. Касательная к описанной
вокруг треугольника АВС окружности, проходит через точку С
и пересекает прямую АВ в точке Р.
а) Докажите, что ВС : АС = СР : АР;
б) Найдите СР, если АМ = 5, ВМ = 4.

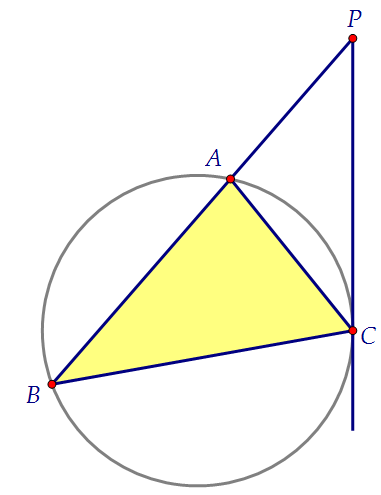В треугольнике АВС проведена биссектриса СМ (вар. 116)

Заметим два подобных треугольника в данной задаче: АРС и СРВ.

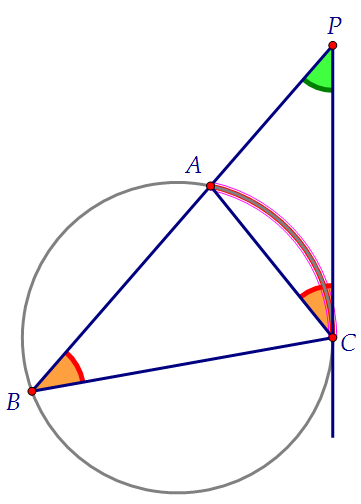Угол Р у треугольников общий, а каждый из красных отмеченных углов равен
половине градусной меры выделенной дуги АС. Составим пропорцию:

$\frac{BC}{CP}=\frac{AC}{AP}$

Отсюда следует и искомое равенство:

$\frac{BC}{AC}=\frac{CP}{AP}$

Проведём биссектрису СМ и пометим данные в условии отрезки:

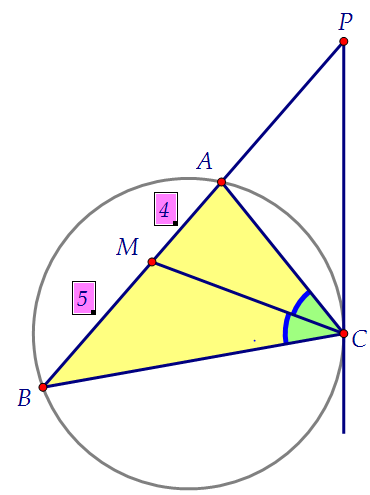В треугольнике АВС проведена биссектриса СМ (вар. 116)

По свойству биссектрисы выполняется следующее равенство:

$\frac{BC}{AC}=\frac{BM}{AM}=\frac{5}{4}$

Воспользуемся доказанной в пункте а) пропорцией:

$\frac{CP}{AP}=\frac{BC}{AC}=\frac{5}{4}$

Обозначим отрезки СР и АР через через 5х и 4х соответственно.

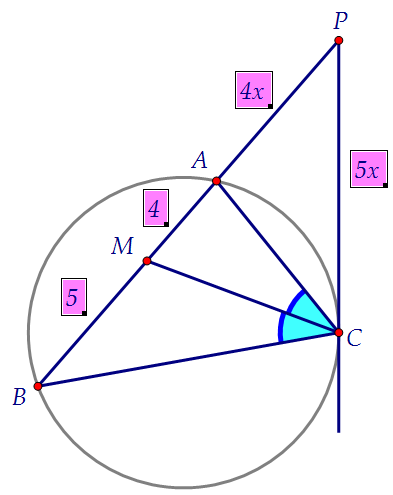Воспользуемся свойством секущих и касательной к окружности:

${PA}\cdot{PB}={PC}^2$

$(4x)\cdot(4x+9)=(5x)^2$

$16x^2+36x=25x^2$

$9x=36$

$x=4$

$PC=5x={5}\cdot{4}=20$

Ответ: 20