Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
18(C5). Система уравнений с параметром (вар. 103)
Комментарии к этой задаче: Комментарий добавил(а): Михаил Можно построить множество в системе координат (х,а) заданное первым неравенством, а также график второго уравнения (параболу). контрольные точки находим, глядя на рисунок Добавить Ваш комментарий: |

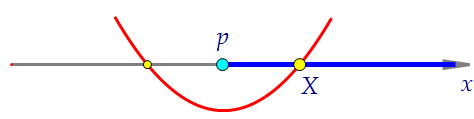 В этом случае необходимо и достаточно решить неравенство f(p) < 0.
2) р - корень уравнения, а вершина параболы расположена левее р.
В этом случае необходимо и достаточно решить неравенство f(p) < 0.
2) р - корень уравнения, а вершина параболы расположена левее р.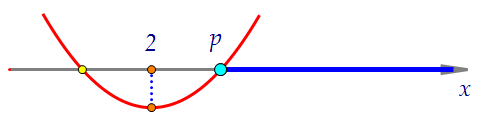 ======================================Займёмся сначала первым случаем, решим неравенство:
======================================Займёмся сначала первым случаем, решим неравенство: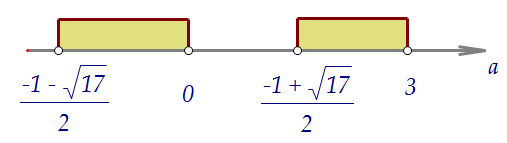 ======================================Второй случай. Просто проверим все четыре значения а.Очевидно, что при а = 0 система имеет два решения.
При а = 3 система имеет единственное решение (какое?)
Т.к. две оставшиеся точки проверить сложнее, можно
пойти сразу другим путём, решив неравенство p ≥ 2.
======================================Второй случай. Просто проверим все четыре значения а.Очевидно, что при а = 0 система имеет два решения.
При а = 3 система имеет единственное решение (какое?)
Т.к. две оставшиеся точки проверить сложнее, можно
пойти сразу другим путём, решив неравенство p ≥ 2.