|
В равнобедренной трапеции АВСD точки М и N – середины оснований ВС и АDсоответственно. Отрезки АМ и ВN пересекаются в точке Р, а отрезки DМ и СN пересекаются в точке К.
а) Докажите, что площадь четырехугольника РМКN равна сумме площадейтреугольников АВР и DСК.
б) Найдите площадь четырехугольника РМКN, если известно, что
ВС = 8, АD = 18, АВ = СD = 13.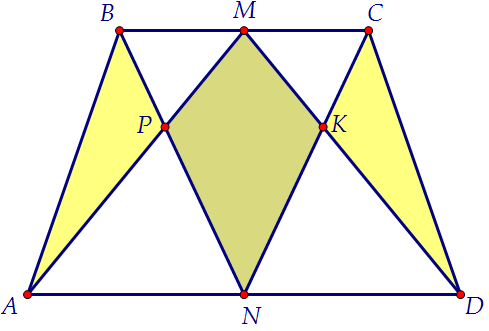 Разрежем трапецию по прямой MN и рассмотрим две новые трапеции:
Разрежем трапецию по прямой MN и рассмотрим две новые трапеции:
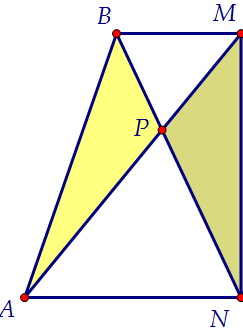  Площади треугольников ABN и AMN равны, т.к. у них равны основания и высоты.Если из каждой площади вычесть площадь их общей части (треугольника APN),то мы получим, что площади цветных треугольников АВР и NMP тоже равны.
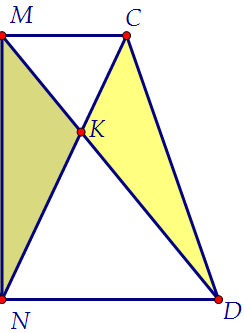
Аналогичные рассуждения проведём и для пары треугольников NMK и DCK.
Четырёхугольник РМКN состоит треугольников NMP и NMP, пункт а) доказан.
!!! положение точек M и N на основаниях трапеции значения пока не имело.=============================================
Теперь учтём, что М и N – середины оснований. Тогда MN - ось симметрии трапеции.
Рассмотрим прямоугольную трапецию АВMN, по данным задачи найдём её высоту 12.
Площади треугольников ABN и AMN равны, т.к. у них равны основания и высоты.Если из каждой площади вычесть площадь их общей части (треугольника APN),то мы получим, что площади цветных треугольников АВР и NMP тоже равны.
Аналогичные рассуждения проведём и для пары треугольников NMK и DCK.
Четырёхугольник РМКN состоит треугольников NMP и NMP, пункт а) доказан.
!!! положение точек M и N на основаниях трапеции значения пока не имело.=============================================
Теперь учтём, что М и N – середины оснований. Тогда MN - ось симметрии трапеции.
Рассмотрим прямоугольную трапецию АВMN, по данным задачи найдём её высоту 12.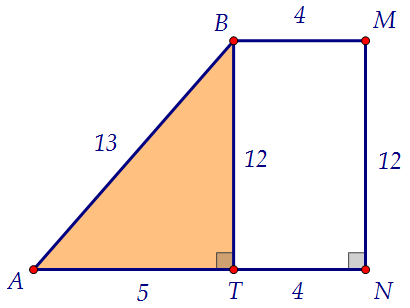 Треугольники ВРМ и NРА подобны, их соответствующие стороны относятся как 4:9.
Значит, площади этих треугольников относятся как 16:25, обозначим их 16х и 25х.
Треугольники МВР и АВР имеют общую высоту, их площади относятся как основания, т.е. 4:9. Значит, площадь АВР равна 36х. Треугольник PMN имеет такую же площадь.
Треугольники ВРМ и NРА подобны, их соответствующие стороны относятся как 4:9.
Значит, площади этих треугольников относятся как 16:25, обозначим их 16х и 25х.
Треугольники МВР и АВР имеют общую высоту, их площади относятся как основания, т.е. 4:9. Значит, площадь АВР равна 36х. Треугольник PMN имеет такую же площадь.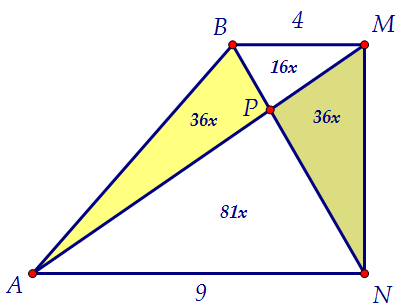 Площадь прямоуг. треугольника AMN равна 0,5·9·12 = 54. Она же равна 117х.
Площадь прямоуг. треугольника AMN равна 0,5·9·12 = 54. Она же равна 117х.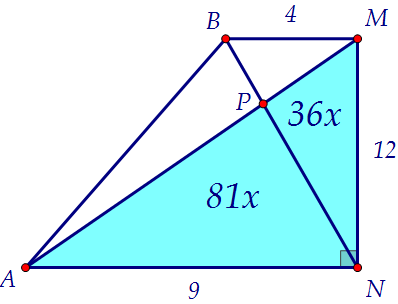 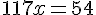 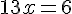 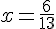 Площадь четырехугольника РМКN равна 72х.
Площадь четырехугольника РМКN равна 72х.
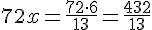 Ответ: Ответ: 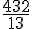 Автор: Ольга Себедаш Просмотров: 9925
|

 Разрежем трапецию по прямой MN и рассмотрим две новые трапеции:
Разрежем трапецию по прямой MN и рассмотрим две новые трапеции:

 Площади треугольников ABN и AMN равны, т.к. у них равны основания и высоты.Если из каждой площади вычесть площадь их общей части (треугольника APN),то мы получим, что площади цветных треугольников АВР и NMP тоже равны.
Аналогичные рассуждения проведём и для пары треугольников NMK и DCK.
Четырёхугольник РМКN состоит треугольников NMP и NMP, пункт а) доказан.
!!! положение точек M и N на основаниях трапеции значения пока не имело.=============================================
Теперь учтём, что М и N – середины оснований. Тогда MN - ось симметрии трапеции.
Рассмотрим прямоугольную трапецию АВMN, по данным задачи найдём её высоту 12.
Площади треугольников ABN и AMN равны, т.к. у них равны основания и высоты.Если из каждой площади вычесть площадь их общей части (треугольника APN),то мы получим, что площади цветных треугольников АВР и NMP тоже равны.
Аналогичные рассуждения проведём и для пары треугольников NMK и DCK.
Четырёхугольник РМКN состоит треугольников NMP и NMP, пункт а) доказан.
!!! положение точек M и N на основаниях трапеции значения пока не имело.=============================================
Теперь учтём, что М и N – середины оснований. Тогда MN - ось симметрии трапеции.
Рассмотрим прямоугольную трапецию АВMN, по данным задачи найдём её высоту 12. Треугольники ВРМ и NРА подобны, их соответствующие стороны относятся как 4:9.
Значит, площади этих треугольников относятся как 16:25, обозначим их 16х и 25х.
Треугольники МВР и АВР имеют общую высоту, их площади относятся как основания, т.е. 4:9. Значит, площадь АВР равна 36х. Треугольник PMN имеет такую же площадь.
Треугольники ВРМ и NРА подобны, их соответствующие стороны относятся как 4:9.
Значит, площади этих треугольников относятся как 16:25, обозначим их 16х и 25х.
Треугольники МВР и АВР имеют общую высоту, их площади относятся как основания, т.е. 4:9. Значит, площадь АВР равна 36х. Треугольник PMN имеет такую же площадь. Площадь прямоуг. треугольника AMN равна 0,5·9·12 = 54. Она же равна 117х.
Площадь прямоуг. треугольника AMN равна 0,5·9·12 = 54. Она же равна 117х.