Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

16(C4). Диаметр и касательные к окружности (вар. 102)

СА и СВ – касательные к окружности в точках А и В соответственно,
АD - её диаметр. Прямые ВD и АС пересекаются в точке Е.
а) Докажите, что точка С – середина отрезка АЕ.
б) Найдите сумму радиусов окружностей, вписанных
в треугольники АВЕ, АВD и АЕD, если ВA = 12.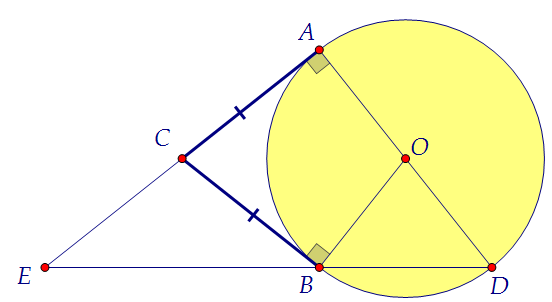

Диаметр и касательные к окружности (вар. 102)

Так как СА и СВ касательные, проведённые к окружности из одной точки С,
то СА = СВ. Кроме того, СА ⊥ ОА и СВ ⊥ ОВ по свойству касательных.

===========================
Посмотрим на задачу с другого конца. Надо доказать, что АС = СЕ.
Значит, в итоге окажутся равными все три отрезка СА = СВ = СЕ.
Такое бывает лишь в прямоугольном треугольнике! Это нам намёк.
===========================

Треугольник АВЕ (и правда!) является прямоугольным, угол АВЕ - прямой.
Это следует из того, что ∠АВD = 90° (впис. угол опирается на диаметр).

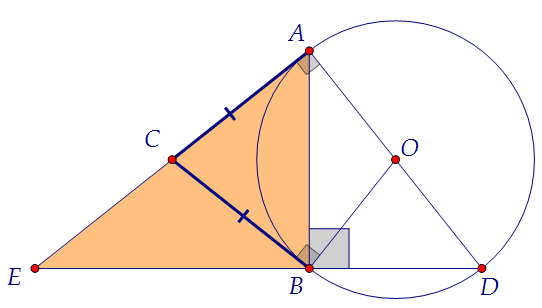Диаметр и касательные к окружности (вар. 102)

А в прямоугольном треугольнике медиана ВС равна половине гипотенузы АЕ
(середина гипотенузы - центр описанной около треугольника окружности).
Таким образом, все три отрезка оказались равными СА = СВ = СЕ, ч.т.д.

Чтобы решить вторую задачу, выразим радиус r вписанной в прямоугольный
треугольник окружности через его катеты а и b и гипотенузу с.

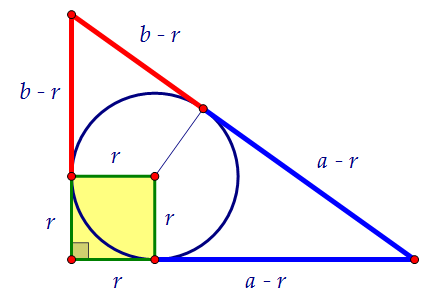
17(C3). Диаметр и касательные к окружности (вар. 102)

$(a - r) + (b - r) = c$

$r=\frac{a+b-c}{2}$

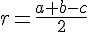Применим полученный результат к данной задаче:

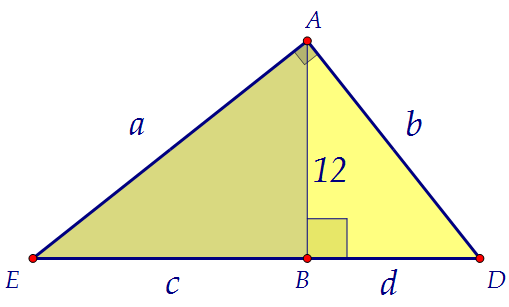Радиус окружности, вписанной в левый треугольник:

$r_1=\frac{c+12-a}{2}$

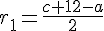Радиус окружности, вписанной в правый треугольник:

$r_2=\frac{d+12-b}{2}$

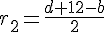Радиус окружности, вписанной в большой треугольник:

$r_3=\frac{a+b-c-d}{2}$

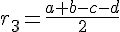Складываем все три радиуса и получаем 12.

Ответ: 12