Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
14(C2). Высота цилиндра равна 15, а радиус равен 2
Комментарии к этой задаче: Комментарий добавил(а): Генка Спасибо! Отлично объяснено, всё понял. Комментарий добавил(а): Алик Туж бадзым тау. Большое спасибо. Комментарий добавил(а): Люба огромное спасибо!! Всё просто и понятно! Комментарий добавил(а): Наталья Спасибо большое за идею , никак не могла догадаться , что центр осеования лежит на высоте теугольника АВС. Комментарий добавил(а): я спасибо прикольно Комментарий добавил(а): Людмила доступное объяснение,спасибо!!! Добавить Ваш комментарий: |

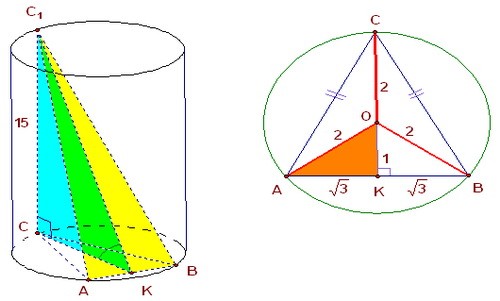 Так как треугольник ABC - равнобедренный, то центр описанной около него окружности
лежит на СК, где СК - медиана, высота, биссектриса и ось симметрии треугольника АВС.
В прямоугольном треугольнике АОК АК = AB/2 = √3, OK = 1 (по теореме Пифагора).
Высота треугольника АВС СК = СО + ОК = 2 + 1 = 3 (т.к. СО - радиус опис. окружности).
Так как треугольник ABC - равнобедренный, то центр описанной около него окружности
лежит на СК, где СК - медиана, высота, биссектриса и ось симметрии треугольника АВС.
В прямоугольном треугольнике АОК АК = AB/2 = √3, OK = 1 (по теореме Пифагора).
Высота треугольника АВС СК = СО + ОК = 2 + 1 = 3 (т.к. СО - радиус опис. окружности).