Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В остроугольном треугольнике АВС высоты АА₁ и СС₁ пересекаются в точке О.
а) Докажите, что треугольники АОС и С₁ОА₁ подобны.
б) Найдите площадь четырехугольника АСА₁С₁, если известно,
что угол АВС равен 30°, a площадь треугольника АВС равна 80.



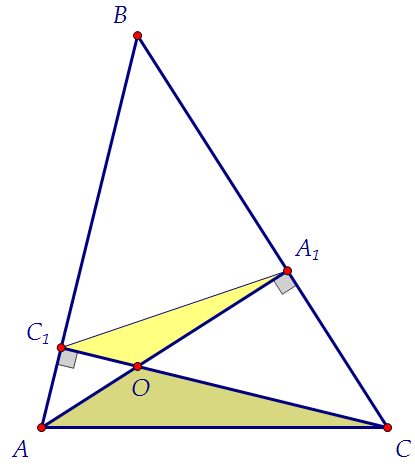Обратим внимание на два прямоугольных треугольника с гипотенузой АС.
Так и хочется описать вокруг них окружность, центр её - середина АС.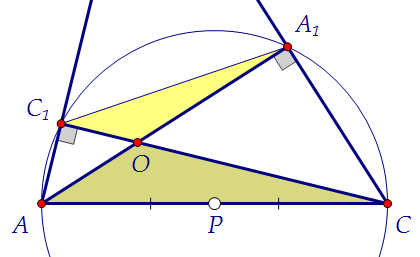



И тут всеми красками заиграют вписанные углы, опирающиеся на дуги.
Красные углы - на красную дугу, зелёные - зелёную. Вписанные углы,
опирающиеся на одну дугу, равны. Имеем две пары равных углов.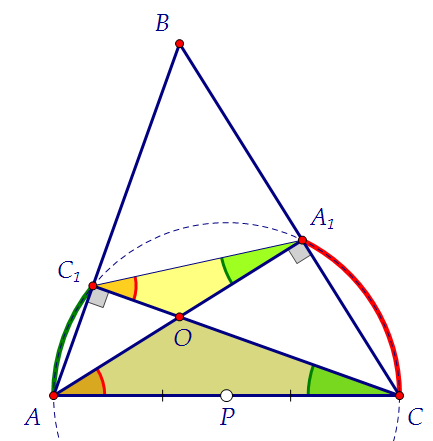



Подобие треугольников по двум углам доказано. Можно было использовать
и вертикальные углы вместо одной пары вписанных.

По ходу дела можно тут же доказать и подобие других треугольников:
АВС и А₁ВС₁. У них есть общий угол и ∠ВС₁А₁ = ∠ВСА, т.к. каждый
из них в сумме с углом АС₁А₁ даёт 180°.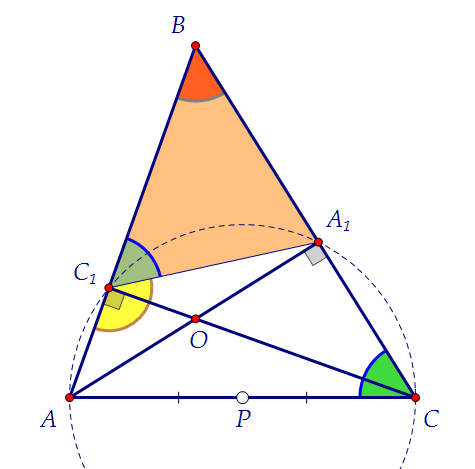



Коэффициент подобия равен отношению соответствующих сторон.



Отношение площадей треугольников равно квадрату коэфф. подобия:



Это означает, что площадь маленького треугольника составляет 3/4
от площади большого. А это значит, что площадь четырёхугольника
АСА₁С₁ составляет 1/4 от площади треугольника АВС, т.е. от 80.

Ответ: 20

Автор: Ольга Себедаш             Просмотров: 28441