Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Две окружности касаются внешним образом в точке А (вар. 97)
Комментарии к этой задаче: Комментарий добавил(а): Tатьяна Откуда HK= (1/5)x O2B ? Комментарий добавил(а): Ольга Себедаш Татьяна, рассмотрите подобные треугольники СНК и СВО2. Комментарий добавил(а): Юлия не понимаю как из подобия СНК и СВО2 нашли НК. мы же не знаем там отрезки Комментарий добавил(а): Юлия всё, поняла:) Комментарий добавил(а): рита спасибо большое Комментарий добавил(а): вариант 97 Можно искать площадь и не через подобие треугольников, из треуг. О2О1Н находим cosО1О2В, затем по теореме косинусов находим АВ, после по теореме Пифагора находим АС, и ищем площадь, как половину произведения катетов. Комментарий добавил(а): Дмитрий Как найдено Ch???? Комментарий добавил(а): ник Круто Комментарий добавил(а): .. Комментарий добавил(а): Комментарий добавил(а): Комментарий добавил(а): @ Комментарий добавил(а): Добавить Ваш комментарий: |
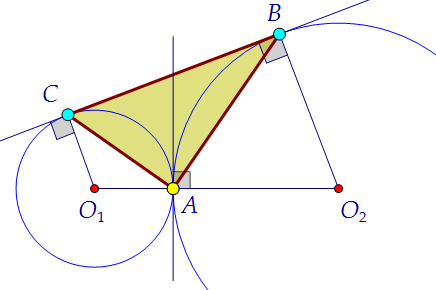Проводя касательные к окружности, не забывайте отмечать ПРЯМЫЕ (!) углы,
которые касательная образует с радиусами, проведёнными в точки касания.
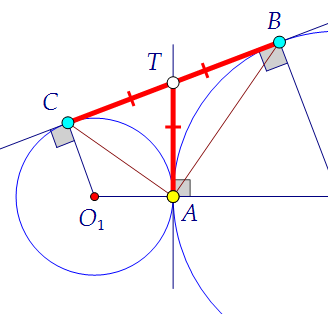ТА и ТС - касательные, проведённые из одной точки Т к маленькой окружности.ТА и ТВ - касательные, проведённые из одной точки Т к большой окружности.По свойству касательных ТА = ТС и ТА = ТВ. Получаем, что ТС = ТВ = ТА.
Таким образом, АТ - медиана треугольника АВС, которая равна половине ВС - стороны, к которой она проведена. Значит, треугольник АВС - прямоугольный.
(т. Т равноудалена от вершин треугольника, т.е. является центром описанной
около АВС окружности. ВС - её диаметр, на диаметр опирается прямой угол).
Чтобы найти площадь треугольника АВС, проведём стандартные вычисления.
В прямоугольной трапеции опустим высоту из вершины тупого угла. Найдём её.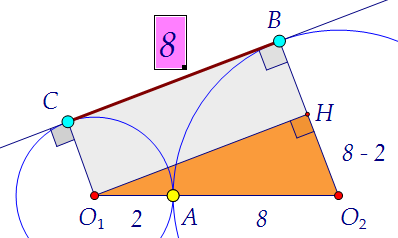
В треугольнике АВС знаем сторону ВС. Для полного счастья не хватает высоты АН.
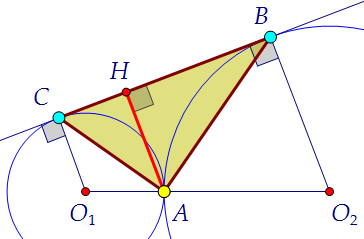Разобьём её на два отрезка АК и КН и найдём каждый из цветных треугольников.
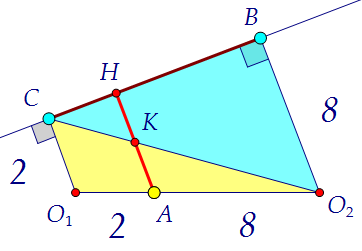Воспользуемся при этом попарным подобием треугольников и данными задачи:
