Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найдите все значения параметра а, при которых система имеет ровно два решения.



Первое уравнение системы перепишем иначе, выделив квадраты двучленов:



Первое слагаемое есть расстояние между точками (x; y) до точки А(-1; 2).
Второе слагаемое есть расстояние между точками (x; y) до точки В(2; 6).
Сумма расстояний от точки (x; y) до двух других должна быть равна 5.



Расстояние между точками А и В легко вычислить, оно равно 5.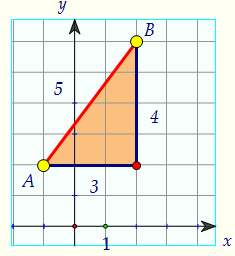



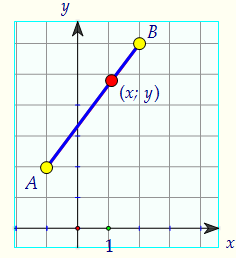
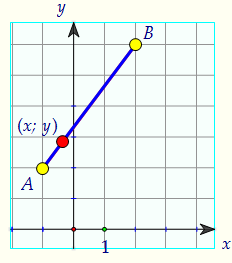Точке (x; y) ничего не остаётся, как лежать на отрезке АВ. Это значит, что
первое уравнение системы задаёт отрезок АВ (отрезок - график уравнения).

Второе уравнение задаёт параболу. Она должна пересекать отрезок в двух точках.
При маленьких а пересечений нет. Первое пересечение возникнет в тот момент,
когда парабола пройдёт через точку А(-1; 2). Найдите это значение а (а = 1).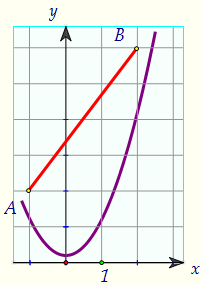

     

Если а капельку увеличить, пересечение останется единственным... до тех пор,
пока парабола не пройдёт через точку В(2; 6). Найдите это значение а (а = 2).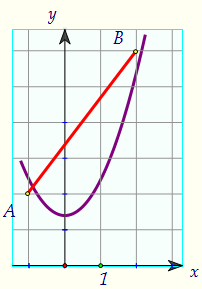

     

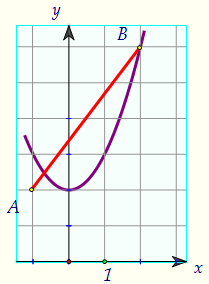Сейчас и с этого момента пересечений ровно два. Но до тех пор, пока...
парабола не коснётся отрезка. Напишем сначала уравнение АВ.

Прямая y = kx + b проходит через А(-1; 2) и В(2; 6). Выполняется система: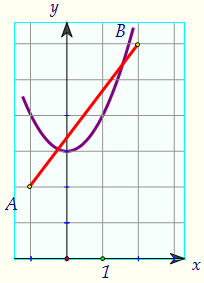



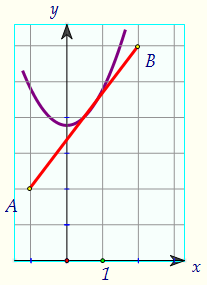Найдя из этой системы значения k и b, напишем уравнение прямой АВ:



Теперь потребуем, чтобы квадратное уравнение имело один корень:











Единственный корень при этом находится в пределах отрезка АВ.

     

При найденном значении параметра решение у начальной системы одно.
При а, больших найденного, пересечений у параболы с отрезком нет.

Ответ: [2; 34/9)

Автор: Ольга Себедаш             Просмотров: 6549