|
В окружность вписан четырехугольник АВСD, диагонали которого перпендикулярны
и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к АВ, пересекает сторону СD в точке М.
а) Докажите, что ЕМ – медиана треугольника СЕD.
б) Найдите длину отрезка ЕМ, если АD = 8, АВ = 4 и угол СDВ равен 60⁰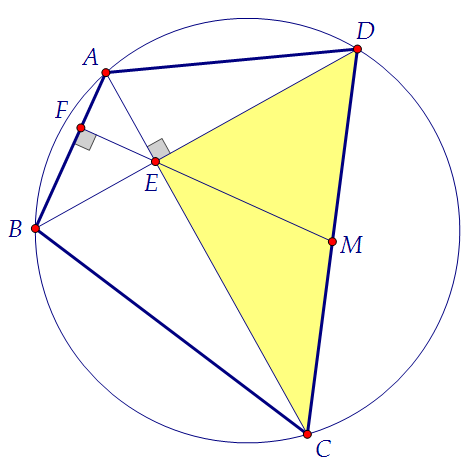 Треугольник CDE прямоугольный. Чтобы доказать, что т. М - середина гипотенузы DC,
достаточно доказать, что т. М - центр описанной около треугольника окружности,т.е. что МЕ = МD = МС. Докажем, что треугольник МDE - равнобедренный.
Треугольник CDE прямоугольный. Чтобы доказать, что т. М - середина гипотенузы DC,
достаточно доказать, что т. М - центр описанной около треугольника окружности,т.е. что МЕ = МD = МС. Докажем, что треугольник МDE - равнобедренный.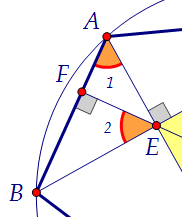 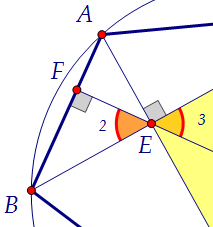 1) ∠1 = ∠2, так как каждый из этих углов в сумме с углом AEF даёт 90°.2) ∠2 = ∠3 как вертикальные. Следовательно, ∠1 = ∠3. Но и это не всё... 1) ∠1 = ∠2, так как каждый из этих углов в сумме с углом AEF даёт 90°.2) ∠2 = ∠3 как вертикальные. Следовательно, ∠1 = ∠3. Но и это не всё...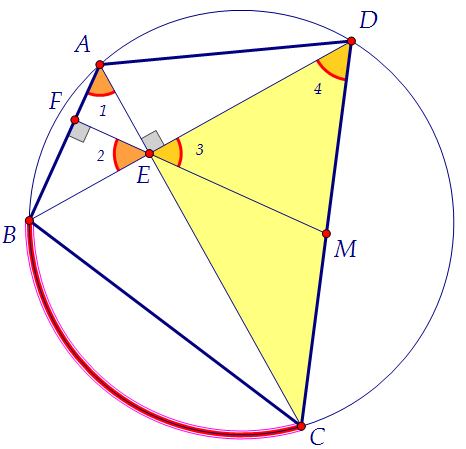 3) ∠1 = ∠4 как опирающиеся на одну и ту же красную дугу. Следовательно, ∠3 = ∠4. По признаку равнобедренного треугольника треугольник МDE равнобедренный.
Аналогично, и треугольник СМЕ равнобедренный. Итак, MD = ME = MC, ч.т.д. 3) ∠1 = ∠4 как опирающиеся на одну и ту же красную дугу. Следовательно, ∠3 = ∠4. По признаку равнобедренного треугольника треугольник МDE равнобедренный.
Аналогично, и треугольник СМЕ равнобедренный. Итак, MD = ME = MC, ч.т.д.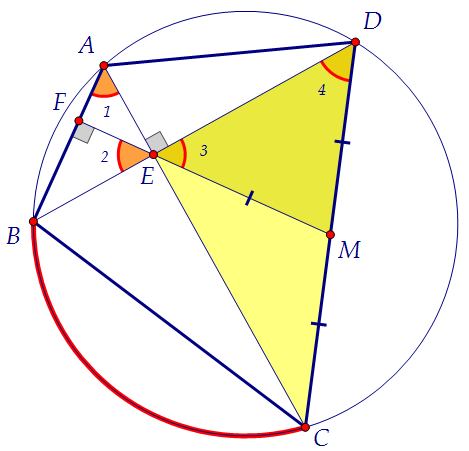 По условию задачи ∠4 = 60°. Это означает, что треугольник МDE равносторонний.Для того, чтобы найти длину отрезка ЕМ, достаточно найти, например, длину ED.Сначала продемонстрирую оригинальный способ. Под ним - стандартный.
По условию задачи ∠4 = 60°. Это означает, что треугольник МDE равносторонний.Для того, чтобы найти длину отрезка ЕМ, достаточно найти, например, длину ED.Сначала продемонстрирую оригинальный способ. Под ним - стандартный.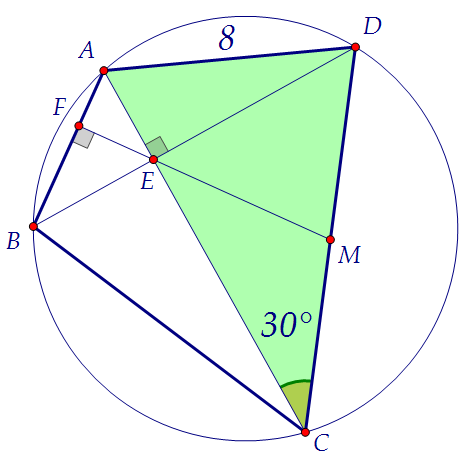 Как только в треугольнике заданы сторона и противолежащий к ней угол, можно сразу найти радиус описанной около треугольника окружности: Как только в треугольнике заданы сторона и противолежащий к ней угол, можно сразу найти радиус описанной около треугольника окружности: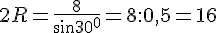 Треугольник ABD вписан в ту же окружность, и у него задана сторона 4.
Треугольник ABD вписан в ту же окружность, и у него задана сторона 4.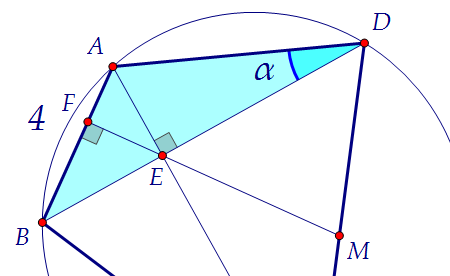 Значит, мы легко можем найти угол, противолежащий этой стороне:
Значит, мы легко можем найти угол, противолежащий этой стороне:
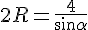
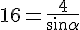
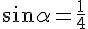
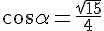 Из прямоугольного треугольника AED можно теперь найти DE.
Из прямоугольного треугольника AED можно теперь найти DE.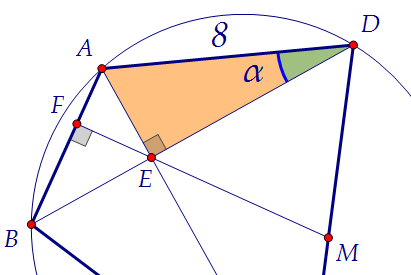
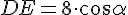
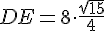
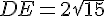 Ответ: 2√15
============================================
Можно действовать и по-другому, учитывая красивые данные углы.
1) Из треугольника АВЕ найдём АЕ = 0,5·8 = 4.
2) Из треугольника ADE найдём DE = 2√15 Ответ: 2√15
============================================
Можно действовать и по-другому, учитывая красивые данные углы.
1) Из треугольника АВЕ найдём АЕ = 0,5·8 = 4.
2) Из треугольника ADE найдём DE = 2√15 Автор: Ольга Себедаш Просмотров: 13781
|

 Треугольник CDE прямоугольный. Чтобы доказать, что т. М - середина гипотенузы DC,
достаточно доказать, что т. М - центр описанной около треугольника окружности,т.е. что МЕ = МD = МС. Докажем, что треугольник МDE - равнобедренный.
Треугольник CDE прямоугольный. Чтобы доказать, что т. М - середина гипотенузы DC,
достаточно доказать, что т. М - центр описанной около треугольника окружности,т.е. что МЕ = МD = МС. Докажем, что треугольник МDE - равнобедренный.
 1) ∠1 = ∠2, так как каждый из этих углов в сумме с углом AEF даёт 90°.2) ∠2 = ∠3 как вертикальные. Следовательно, ∠1 = ∠3. Но и это не всё...
1) ∠1 = ∠2, так как каждый из этих углов в сумме с углом AEF даёт 90°.2) ∠2 = ∠3 как вертикальные. Следовательно, ∠1 = ∠3. Но и это не всё... 3) ∠1 = ∠4 как опирающиеся на одну и ту же красную дугу. Следовательно, ∠3 = ∠4. По признаку равнобедренного треугольника треугольник МDE равнобедренный.
Аналогично, и треугольник СМЕ равнобедренный. Итак, MD = ME = MC, ч.т.д.
3) ∠1 = ∠4 как опирающиеся на одну и ту же красную дугу. Следовательно, ∠3 = ∠4. По признаку равнобедренного треугольника треугольник МDE равнобедренный.
Аналогично, и треугольник СМЕ равнобедренный. Итак, MD = ME = MC, ч.т.д. По условию задачи ∠4 = 60°. Это означает, что треугольник МDE равносторонний.Для того, чтобы найти длину отрезка ЕМ, достаточно найти, например, длину ED.Сначала продемонстрирую оригинальный способ. Под ним - стандартный.
По условию задачи ∠4 = 60°. Это означает, что треугольник МDE равносторонний.Для того, чтобы найти длину отрезка ЕМ, достаточно найти, например, длину ED.Сначала продемонстрирую оригинальный способ. Под ним - стандартный. Как только в треугольнике заданы сторона и противолежащий к ней угол, можно сразу найти радиус описанной около треугольника окружности:
Как только в треугольнике заданы сторона и противолежащий к ней угол, можно сразу найти радиус описанной около треугольника окружности: Значит, мы легко можем найти угол, противолежащий этой стороне:
Значит, мы легко можем найти угол, противолежащий этой стороне:
