Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В треугольнике АВС на стороне ВС выбрана точка К так, что СК : ВК = 1 : 2.
Точка Е – середина стороны АВ. Отрезки СЕ и АК пересекаются в точке Р.
а) Докажите, что треугольники ВРС и АРС имеют равные площади.
б) Найдите площадь треугольника АВР, если площадь
треугольника АВС равна 120.

Утверждение пункта а) выполняется независимо от положения точки Р на медиане СЕ.



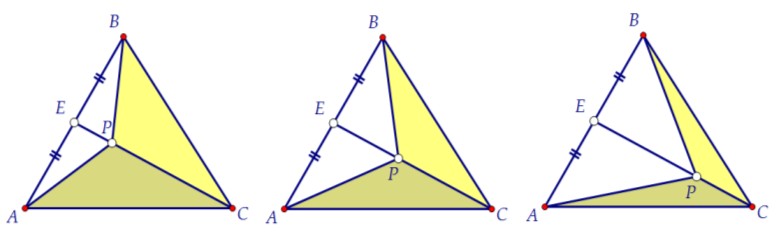Медиана всегда делит треугольник на два равновеликих треугольника (почему?).
Площади треугольников ВСЕ и АСЕ равны (СЕ - медиана треугольника АВС).
Площади треугольников ВРЕ и АРЕ равны (РЕ - медиана треугольника АВР).
Поэтому и площади треугольников ВРС и АРС равны как разности (чего?).

Но для решения пункта б) нам понадобится полное условие.

Отрезок РЕ делит площадь треугольника АРВ в отношении 1 : 1.
Отрезок РК делит площадь треугольника ВРС в отношении 2 : 1.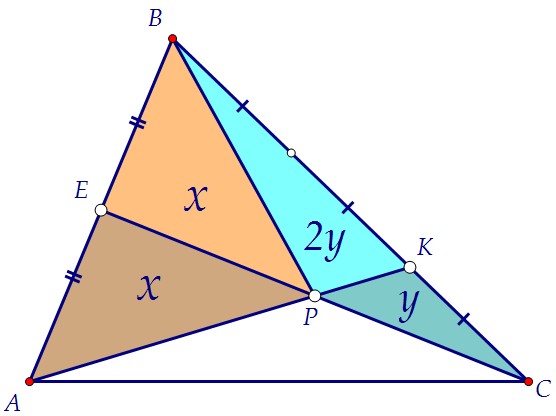



Мы доказали, что площадь треугольника АРС равна площади ВРС.



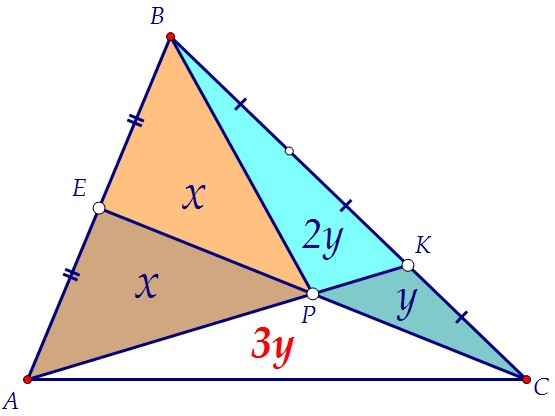Отрезок РК делит площадь треугольника АВС в отношении 2 : 1.



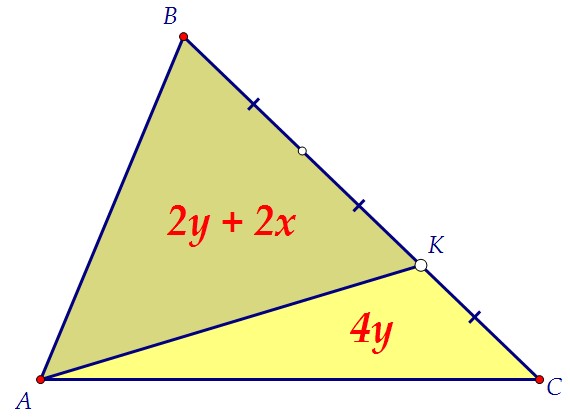Получаем следующую связку между введёнными переменными х и y:



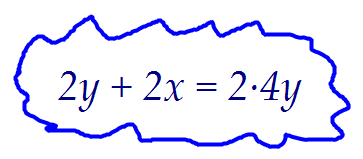Отсюда получаем, что х = 3y. Площадь треугольника АВС равна 12y.
Так как по условию площадь треугольника АВС равна 120, то y = 10.
Теперь легко найти и площадь треугольника АВР, которая равна 6y.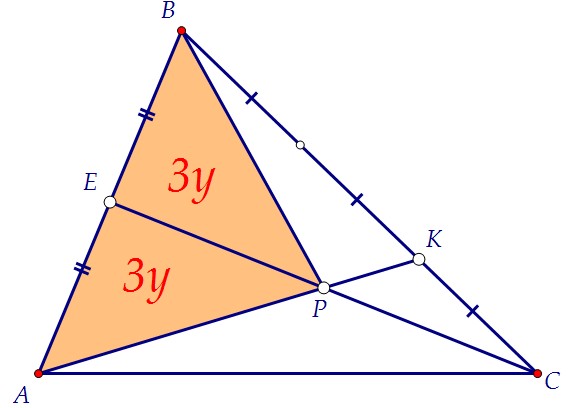



Ответ: 60

Автор: Ольга Себедаш             Просмотров: 13291