|
В треугольнике ABC AB = 20, AC = 24. Окружность с центром O2 на стороне AC проходит через вершину С, точку пересечения биссектрисы угла А со стороной BC и центр O1 вписанной в треугольник ABC окружности.а) Докажите, что прямая O1O2 параллельна прямой BC;б) Найдите радиус описанной около треугольника ABC окружности.
Центр O1 вписанной в треугольник АВС окружности - точка пересечения биссектрис треугольника, т.е. O1 лежит на биссектрисе АР, и СO1 - биссектриса угла С.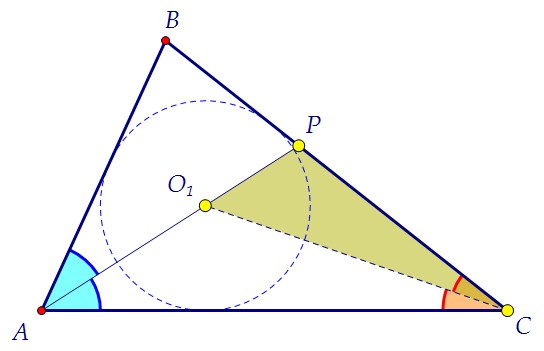 Вторая окружность проходит через точки O1 и С, значит, её центр O2 лежит на серединном перпендикуляре к отрезку O1С. По условию O2 лежит и на АС. Вторая окружность проходит через точки O1 и С, значит, её центр O2 лежит на серединном перпендикуляре к отрезку O1С. По условию O2 лежит и на АС.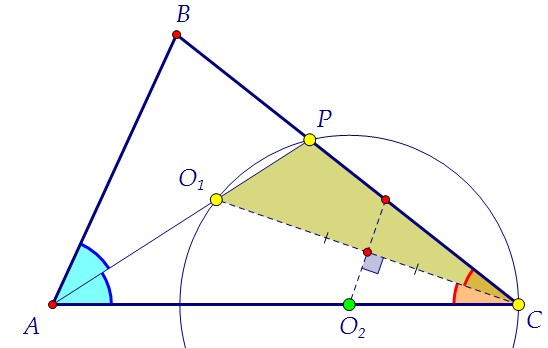 O2 равноудалена от точек O1 и С, треугольник O1O2С равнобедренный, углы при основании равнобедренного треугольника равны (∠2 = ∠3). O2 равноудалена от точек O1 и С, треугольник O1O2С равнобедренный, углы при основании равнобедренного треугольника равны (∠2 = ∠3). 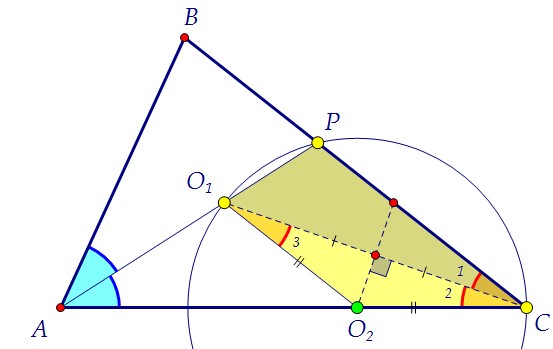 Итак, ∠1 = ∠2 и ∠2 = ∠3. Значит, ∠1 = ∠3. Т.к. внутренние накрест лежащие углы при прямых O1O2 и ВС и секущей O1С равны, то прямые параллельны по признаку параллельности прямых, что и требовалось доказать.*** Заметьте! Факт прохождения окружности через точку Р был здесь лишним.И условие о том, что АР является биссектрисой, мы тоже ещё не использовали.Но для дальнейшего решения точку Р необходимо использовать. Заметим, что треугольники O1O2Р и ТСO2 равны по двум сторонам и углу между ними. Итак, ∠1 = ∠2 и ∠2 = ∠3. Значит, ∠1 = ∠3. Т.к. внутренние накрест лежащие углы при прямых O1O2 и ВС и секущей O1С равны, то прямые параллельны по признаку параллельности прямых, что и требовалось доказать.*** Заметьте! Факт прохождения окружности через точку Р был здесь лишним.И условие о том, что АР является биссектрисой, мы тоже ещё не использовали.Но для дальнейшего решения точку Р необходимо использовать. Заметим, что треугольники O1O2Р и ТСO2 равны по двум сторонам и углу между ними. 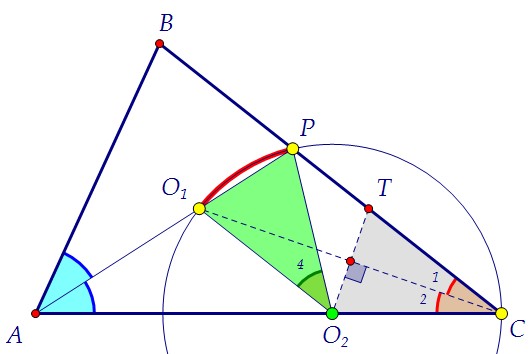 Зелёный является равнобедренным, его боковые стороны - радиусы окружности. В сером биссектриса является высотой, и его боковые стороны равны радиусу. Легко заметить, что углы между боковыми сторонами в треугольниках равны. Угол 1 - вписанный и равен половине красной дуги, на которую он опирается, а значит, половине центрального угла 4. Но ∠1 = ∠2, поэтому ∠1 + ∠2 = ∠4.Из равенства треугольников следует равенство их оснований O1Р = O2Т,а также углов при основании. Точка Р, таким образом, свою роль сыграла.Используем теперь доказанную параллельность прямых O1O2 и ВС. Зелёный является равнобедренным, его боковые стороны - радиусы окружности. В сером биссектриса является высотой, и его боковые стороны равны радиусу. Легко заметить, что углы между боковыми сторонами в треугольниках равны. Угол 1 - вписанный и равен половине красной дуги, на которую он опирается, а значит, половине центрального угла 4. Но ∠1 = ∠2, поэтому ∠1 + ∠2 = ∠4.Из равенства треугольников следует равенство их оснований O1Р = O2Т,а также углов при основании. Точка Р, таким образом, свою роль сыграла.Используем теперь доказанную параллельность прямых O1O2 и ВС.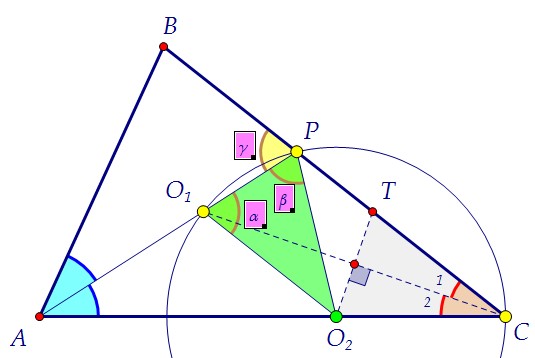 По свойству параллельных прямых α = γ. А так как α = β, то β = γ.Используем, наконец, равенство голубых углов ВАР и САР. По свойству параллельных прямых α = γ. А так как α = β, то β = γ.Используем, наконец, равенство голубых углов ВАР и САР.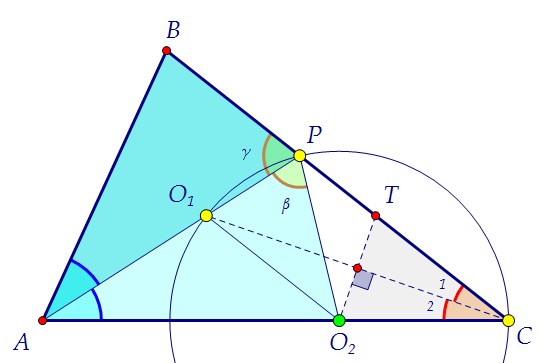 Треугольники ВАР и O2АР равны стороне и двум прилежащим к ней углам.Следовательно, РВ = РO2 как соответствующие. И появляется на сцене ... Треугольники ВАР и O2АР равны стороне и двум прилежащим к ней углам.Следовательно, РВ = РO2 как соответствующие. И появляется на сцене ...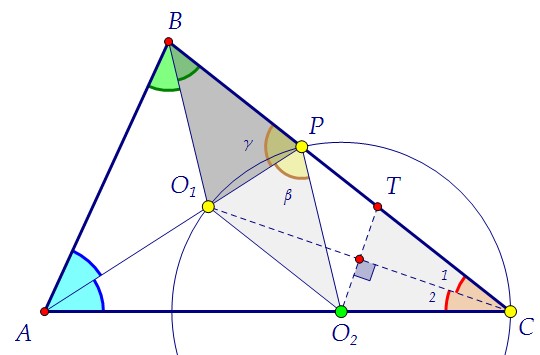 ... третий серый треугольник ВO1Р. Он равен треугольнику O1РO2 по двум сторонам и углу между ними. ∠O1ВР = ∠АСТ как соответствующие. Но!Угол O1ВР равен половине угла АВС. В треугольнике АВС ∠В = 2·∠С.Использовать этот факт можно с помощью теоремы синусов: ... третий серый треугольник ВO1Р. Он равен треугольнику O1РO2 по двум сторонам и углу между ними. ∠O1ВР = ∠АСТ как соответствующие. Но!Угол O1ВР равен половине угла АВС. В треугольнике АВС ∠В = 2·∠С.Использовать этот факт можно с помощью теоремы синусов: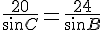
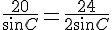
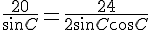
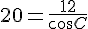

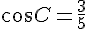 Для поиска же радиуса описанной окружности требуется синус угла С:
Для поиска же радиуса описанной окружности требуется синус угла С:
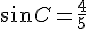
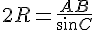
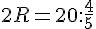
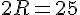
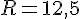 Ответ: 12,5 Ответ: 12,5 Автор: Ольга Себедаш Просмотров: 12084
|

 Вторая окружность проходит через точки O1 и С, значит, её центр O2 лежит на серединном перпендикуляре к отрезку O1С. По условию O2 лежит и на АС.
Вторая окружность проходит через точки O1 и С, значит, её центр O2 лежит на серединном перпендикуляре к отрезку O1С. По условию O2 лежит и на АС. O2 равноудалена от точек O1 и С, треугольник O1O2С равнобедренный, углы при основании равнобедренного треугольника равны (∠2 = ∠3).
O2 равноудалена от точек O1 и С, треугольник O1O2С равнобедренный, углы при основании равнобедренного треугольника равны (∠2 = ∠3).  Итак, ∠1 = ∠2 и ∠2 = ∠3. Значит, ∠1 = ∠3. Т.к. внутренние накрест лежащие углы при прямых O1O2 и ВС и секущей O1С равны, то прямые параллельны по признаку параллельности прямых, что и требовалось доказать.*** Заметьте! Факт прохождения окружности через точку Р был здесь лишним.И условие о том, что АР является биссектрисой, мы тоже ещё не использовали.Но для дальнейшего решения точку Р необходимо использовать. Заметим, что треугольники O1O2Р и ТСO2 равны по двум сторонам и углу между ними.
Итак, ∠1 = ∠2 и ∠2 = ∠3. Значит, ∠1 = ∠3. Т.к. внутренние накрест лежащие углы при прямых O1O2 и ВС и секущей O1С равны, то прямые параллельны по признаку параллельности прямых, что и требовалось доказать.*** Заметьте! Факт прохождения окружности через точку Р был здесь лишним.И условие о том, что АР является биссектрисой, мы тоже ещё не использовали.Но для дальнейшего решения точку Р необходимо использовать. Заметим, что треугольники O1O2Р и ТСO2 равны по двум сторонам и углу между ними.  Зелёный является равнобедренным, его боковые стороны - радиусы окружности. В сером биссектриса является высотой, и его боковые стороны равны радиусу. Легко заметить, что углы между боковыми сторонами в треугольниках равны. Угол 1 - вписанный и равен половине красной дуги, на которую он опирается, а значит, половине центрального угла 4. Но ∠1 = ∠2, поэтому ∠1 + ∠2 = ∠4.Из равенства треугольников следует равенство их оснований O1Р = O2Т,а также углов при основании. Точка Р, таким образом, свою роль сыграла.Используем теперь доказанную параллельность прямых O1O2 и ВС.
Зелёный является равнобедренным, его боковые стороны - радиусы окружности. В сером биссектриса является высотой, и его боковые стороны равны радиусу. Легко заметить, что углы между боковыми сторонами в треугольниках равны. Угол 1 - вписанный и равен половине красной дуги, на которую он опирается, а значит, половине центрального угла 4. Но ∠1 = ∠2, поэтому ∠1 + ∠2 = ∠4.Из равенства треугольников следует равенство их оснований O1Р = O2Т,а также углов при основании. Точка Р, таким образом, свою роль сыграла.Используем теперь доказанную параллельность прямых O1O2 и ВС. По свойству параллельных прямых α = γ. А так как α = β, то β = γ.Используем, наконец, равенство голубых углов ВАР и САР.
По свойству параллельных прямых α = γ. А так как α = β, то β = γ.Используем, наконец, равенство голубых углов ВАР и САР. Треугольники ВАР и O2АР равны стороне и двум прилежащим к ней углам.Следовательно, РВ = РO2 как соответствующие. И появляется на сцене ...
Треугольники ВАР и O2АР равны стороне и двум прилежащим к ней углам.Следовательно, РВ = РO2 как соответствующие. И появляется на сцене ... ... третий серый треугольник ВO1Р. Он равен треугольнику O1РO2 по двум сторонам и углу между ними. ∠O1ВР = ∠АСТ как соответствующие. Но!Угол O1ВР равен половине угла АВС. В треугольнике АВС ∠В = 2·∠С.Использовать этот факт можно с помощью теоремы синусов:
... третий серый треугольник ВO1Р. Он равен треугольнику O1РO2 по двум сторонам и углу между ними. ∠O1ВР = ∠АСТ как соответствующие. Но!Угол O1ВР равен половине угла АВС. В треугольнике АВС ∠В = 2·∠С.Использовать этот факт можно с помощью теоремы синусов: