|
Найдите все значения параметра а, при каждом из которых система
имеет ровно одно решение.
Значение а = 0 можно проверить сходу и далее рассматривать а ≠ 0.
Преобразуем первое уравнение системы:
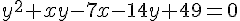
^2+x(y-7)=0)
(y-7+x)=0)
Сдвинем все графики на единичку вниз, чтобы парабола стала удобнее.
Решение, постановка вопроса и ответ на него от сдвига не изменятся.
(y-6+x)=0 \\
y=ax^2 \\
x\geq3
\end{array}
\right)
Построим два луча y = 6 и y = 6 - x при x ≥ 3 и параболу y = ax2.
Если ветви параболы направлены вверх, возможны три варианта:
1) Парабола не пересекает ни один из лучей (например, y = x2, y = 2x2):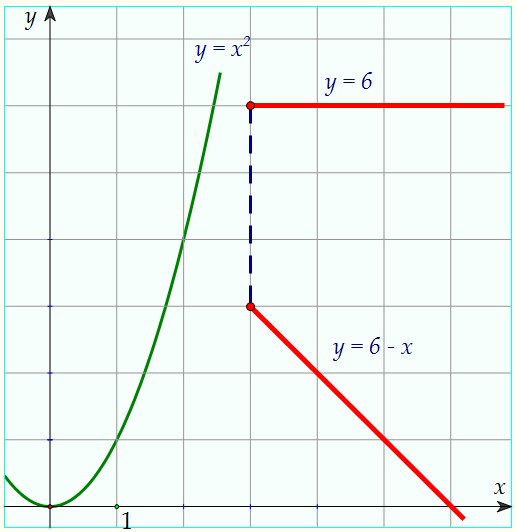
2) Парабола проходит через начало верхнего луча y = 6, т.е. через точку (3; 6):
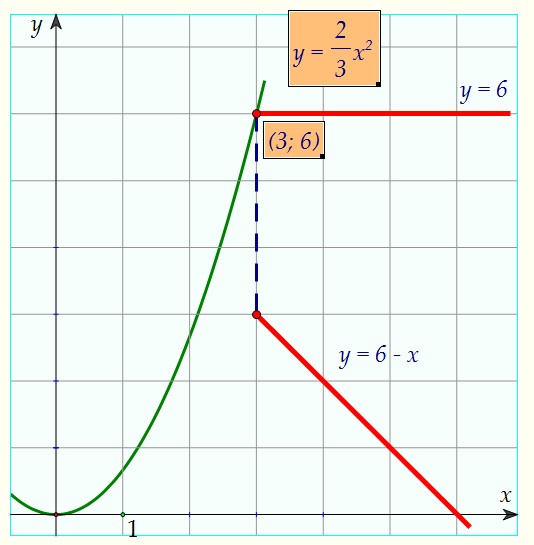3) Парабола проходит через начало нижнего луча y = 6 - x, т.е. через точку (3; 3):
В первом случае (a > 2/3) система не имеет решений, во втором случае (a = 2/3)
решение единственно, в третьем случае (a = 1/3) решений ровно два.
Очевидно, что если 0 < a < 1/3, то решений тоже два. Единственное решение
будет у системы и в случае, если 1/3 < a < 2/3 (например, y = 0,5x2):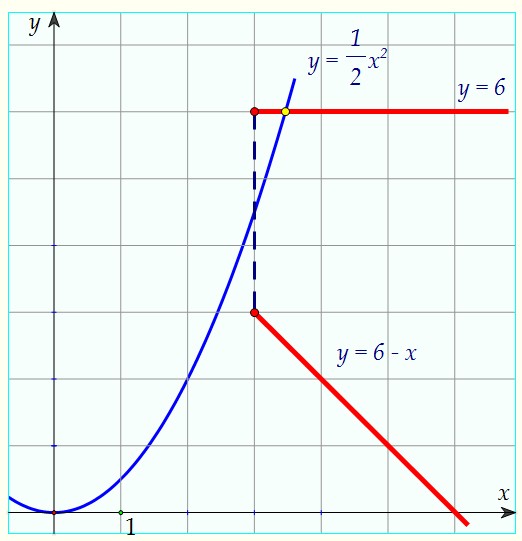
Если ветви параболы направлены вниз, то пересечь верхний луч (y = 6)
она не сможет, а нижнего луча (y = 6 - x) имеет право лишь коснуться.
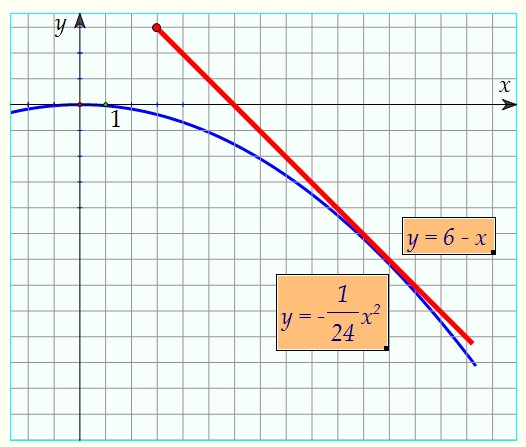Чтобы найти значение параметра а, при котором происходит касание,
достаточно потребовать, чтобы квадратное уравнение
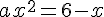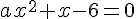имело единственное решение, не меньшее трёх.
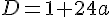
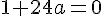
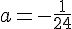При найденном а найдём корень (он не должен оказаться меньше трёх):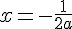
)
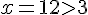Ответ:  ; 
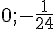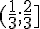Автор: Ольга Себедаш Просмотров: 14812
|
