Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

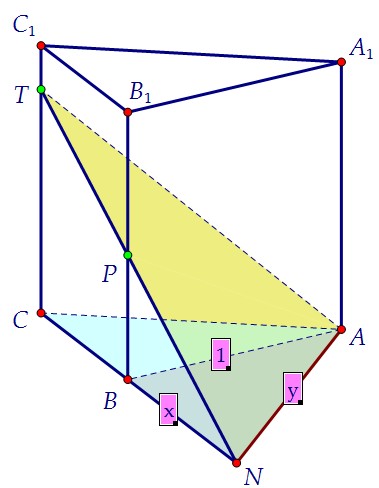
14(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

На боковых ребрах АА₁, ВВ₁ и СС₁ правильной треугольной призмы АВСА₁В₁С₁
(АА₁ || ВВ₁ || СС₁) расположены точки К, L, и М соответственно. Известно, что
угол между прямыми KL и АВ равен π/4, а угол между прямыми КМ и АС - π/3.
а) Постройте плоскость, проходящую через точки K, L и М.
б) Найдите угол между этой плоскостью и плоскостью основания АВС.

На боковых рёбрах правильной треугольной призмы (вар. 91)

Параллельно сдвинем плоскость KLM вниз, так чтобы точка К оказалась в точке А.
Ответ задачи от этого переноса не изменится, но рассуждать станет проще.

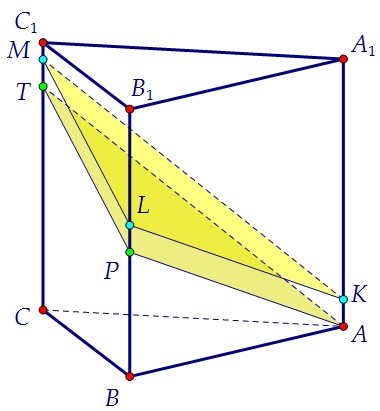16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

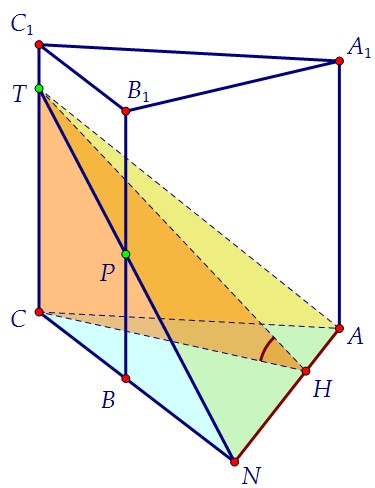
Найдём ребро двугранного угла. Для этого пересечём ТР и СВ, получим точку N.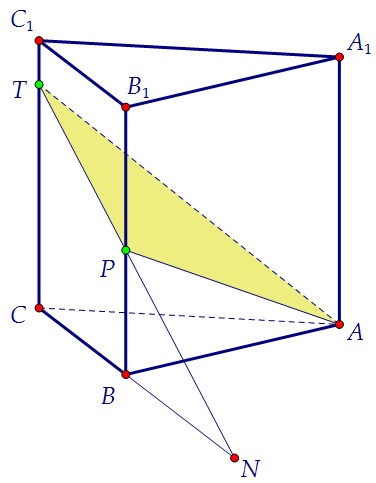

Плоскости РТК и АВС пересекаются по прямой AN - это и есть ребро двугранного угла.

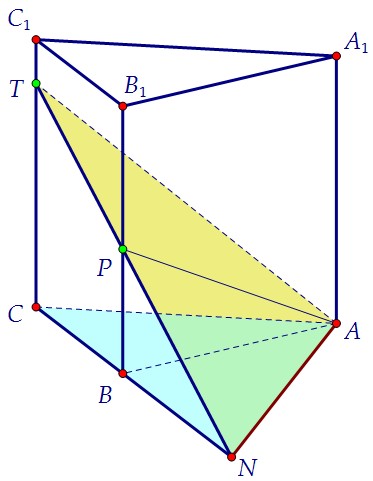16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

Искомый угол ТНС (линейный) - угол между перпендикулярами к этому ребру.

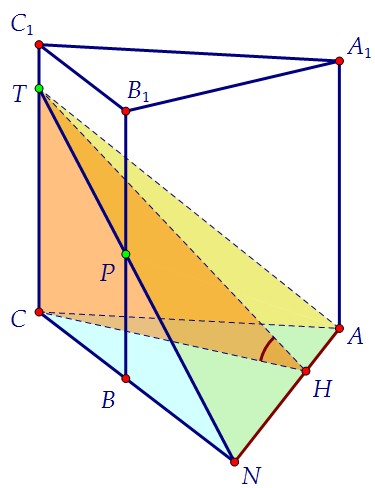Чтобы его построить, надо опустить перпендикуляр СН к АN в плоскости АВС.
По теореме о трёх перпендикулярах ТН тоже окажется перпендикуляром к AN.
Из треугольника СТН мы и найдём тангенс угла ТНС. Но нужно знать стороны.

Пусть сторона основания равна 1. Для чего дан угол π/3? Чтобы мы увидели
стандартный прямоугольный треугольник с углом 30° и нашли его стороны.

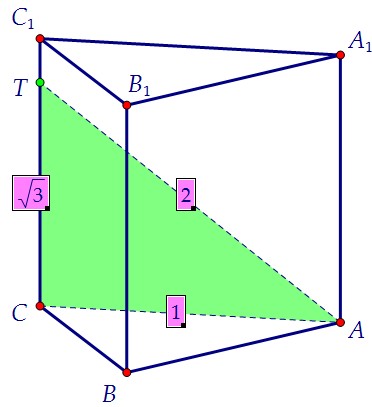16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

Для чего дан угол π/4? Чтобы мы увидели другой не менее стандартный
прямоугольный треугольник с углами 45° и тоже нашли его стороны.

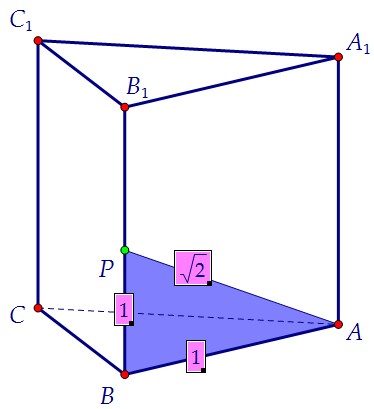16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

Для нахождения тангенса искомого угла один катет у нас уже есть: СТ = √3.
Другой катет СН - высота треугольника ACN. Чтобы её найти, надо знать
площадь треугольника и основание AN. Начнём с поиска стороны CN.

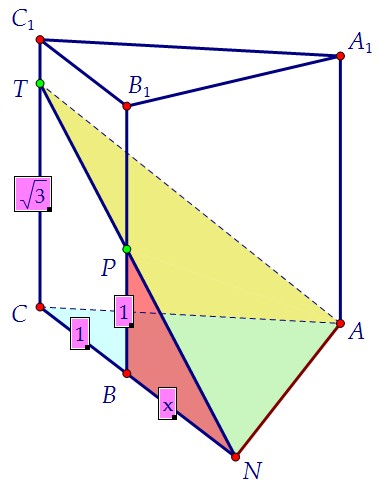16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

Обозначим отрезок BN = х и воспользуемся подобием треугольников BPN и CTN:

$\frac{x}{x+1}=\frac{1}{\sqrt{3}}$

$x+1=x\sqrt{3}$

$x=\frac{1}{\sqrt{3}-1}$

$CN=x+1=\frac{1}{\sqrt{3}-1}+1=\frac{\sqrt{3}}{\sqrt{3}-1}$

Из треугольника BАN по теореме косинусов найдём сторону АN (напротив 120°).

16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

$y^2=x^2+1-{2}\cdot{x}\cdot{(-0,5)}=x^2+x+1$

$y^2=\frac{1}{(\sqrt{3}-1)^2}+\frac{1}{\sqrt{3}-1}+1$

$y^2=\frac{(\sqrt{3}-1)^2+(\sqrt{3}-1)+1}{(\sqrt{3}-1)^2}$

$y^2=\frac{4-\sqrt{3}}{4-2\sqrt{3}}$

Площадь треугольника ACN можно искать двумя разными способами:

$S={\frac{1}{2}}\cdot{CN}\cdot{CA}\cdot{sin60^0}={\frac{1}{2}}\cdot{(x+1)}\cdot{1}\cdot{\frac{\sqrt{3}}{2}}={\frac{1}{2}}\cdot{(x+1)}\cdot{\frac{\sqrt{3}}{2}}$

С другой стороны, можно использовать найденное основание AN:

$S={\frac{1}{2}}\cdot{y}\cdot{CH}$

Приравняв полученные площади, найдём неизвестную высоту:

${(x+1)}\cdot{\frac{\sqrt{3}}{2}}={y}\cdot{CH}$

${\frac{\sqrt{3}}{\sqrt{3}-1}}\cdot{\frac{\sqrt{3}}{2}}={\sqrt{\frac{4-\sqrt{3}}{4-2\sqrt{3}}}}\cdot{CH}$

${\frac{1}{\sqrt{3}-1}}\cdot{\frac{3}{2}}={\frac{\sqrt{4-\sqrt{3}}}{\sqrt{3}-1}}\cdot{CH}$

$\frac{3}{2}={\sqrt{4-\sqrt{3}}}\cdot{CH}$

$CH=\frac{3}{2\sqrt{4-\sqrt{3}}}$

Осталось найти тангенс искомого угла между плоскостями.

16(C2). На боковых рёбрах правильной треугольной призмы (вар. 91)

$tg{\alpha}=\frac{CT}{CH}={\sqrt{3}}\cdot{\frac{2\sqrt{4-\sqrt{3}}}{3}}=\frac{2\sqrt{4-\sqrt{3}}}{\sqrt{3}}=2\sqrt{\frac{4}{3}-\frac{1}{\sqrt{3}}}$