Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

18(C5). Найдите все значения а, при которых уравнение имеет ровно три корня (вар. 90)

Найдите все значения а, при которых уравнение имеет ровно три корня.

$|9^{\sqrt{x}}-{2(a+5)}\cdot{3^{\sqrt{x}}}+9a+19|=2a^2+a+2$

Сделаем очевидную замену t = 3^√x и заметим, что t ≥ 1, т.к. √х ≥ 0.

$|t^2-{2(a+5)}\cdot{t}+9a+19|=2a^2+a+2$ ***

Рассмотрим квадратный трёхчлен под знаком модуля.

$y=t^2-{2(a+5)}\cdot{t}+9a+19$

Найдём координаты вершины параболы:

$x_0=a+5$
$y_0=(a+5)^2-{2(a+5)}\cdot{(a+5)}+9a+19=-a^2-a-6<0$

Если бы t принимало любые значения, парабола пересекала бы ось ОХ
в двух точках. А график левой части уравнения *** выглядел бы так:

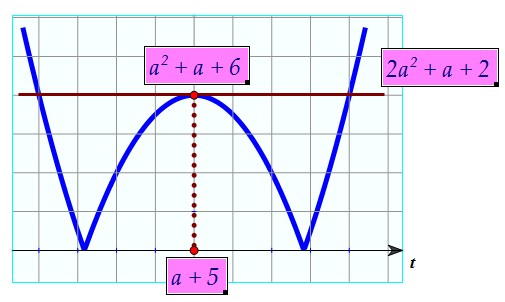20(C5). Найдите все значения а, при которых уравнение имеет ровно три корня (вар. 90)

В этом случае только одна горизонтальная прямая пересекает график
ровно в трёх точках. И нам достаточно было бы решить уравнение:

$a^2+a+6=2a^2+a+2$

$a^2=4$

$a=\pm2$

Но t ≥ 1. Если 1 находится левее вершины и f(1) ≥ a² + a + 6,
то ситуация аналогична только что рассмотренной.

$f(x)=|t^2-{2(a+5)}\cdot{t}+9a+19|$

$f(1)=|1-{2(a+5)}+9a+19|=|7a+10|$

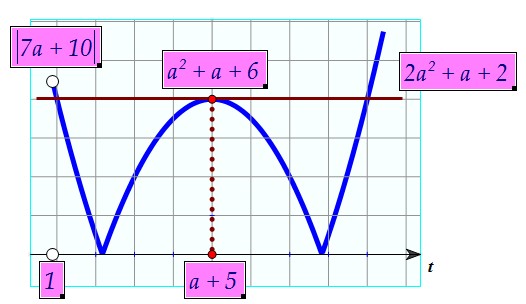20(C5). Найдите все значения а, при которых уравнение имеет ровно три корня (вар. 90)

Числа 2 и -2 достаточно подвергнуть проверке выполнения двух условий:

$\left\{ \begin{array}{rcl} a+5>1 \\ {|7a+10|}\geq{a^2+a+6} \\ \end{array} \right$

Этим условиям удовлетворяет только а = 2. Это значение войдёт в ответ.

==========================================

Но три корня могут быть и в случае, когда 1 по-прежнему левее вершины,
но f(1) < a² + a + 6. Картинка при этом выглядит так:

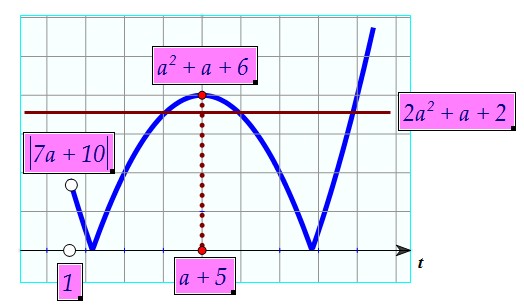
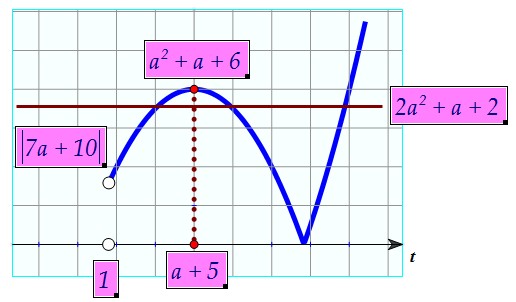20(C5). Найдите все значения а, при которых уравнение имеет ровно три корня (вар. 90)

В этом случае прямая y = 2a² + a + 2 должна оказаться
строго между прямыми y = |7a + 10| и y = a² + a + 6

$\left\{ \begin{array}{rcl} a+5>1 \\ |7a+10|<a^2+a+6 \\ 2a^2+a+2>|7a+10| \\ 2a^2+a+2<a^2+a+6 \\ \end{array} \right$

$\left\{ \begin{array}{rcl} a+5>1 \\ 7a+10<a^2+a+6 \\ 7a+10>-a^2-a-6 \\ 7a+10<2a^2+a+2 \\ 7a+10>-2a^2-a-2 \\ 2a^2+a+2<a^2+a+6 \\ \end{array} \right$

$\left\{ \begin{array}{rcl} a+5>1 \\ a^2-6a-4>0 \\ a^2+8a+16>0 \\ a^2-3a-4>0 \\ a^2+4a+6>0 \\ a^2-4<0 \\ \end{array} \right$

$\left\{ \begin{array}{rcl} a^2-6a-4>0 \\ a^2-3a-4>0 \\ -2<a<2 \\ \end{array} \right$

Решением этой системы является интервал (-2; -1).

Ответ: (-2; -1); 2