|
В треугольнике ABC точка О - центр описанной окружности, точка К лежит на отрезке ВС, причем BК = КC. Описанная около треугольника BКO
окружность пересекает АВ в точке Т.
а) Докажите, что TК || АС.
б) Найдите площадь треугольника ABC, если известно, что угол BOК равен 30°, КT = 8, ВТ = 6.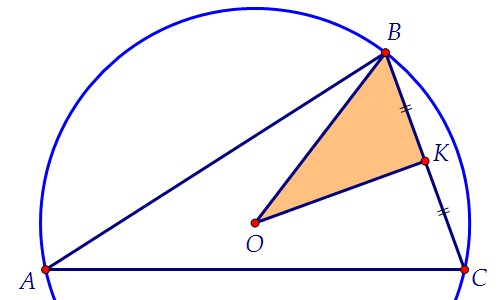 Центр описанной около треугольника АВС окружности равноудалён от его вершин,то есть является точкой пересечения серединных перпендикуляров к его сторонам.По условию К - середина ВС. Значит, ОК ⊥ ВС и треугольник ВКО прямоугольный.Центр Р окружности, описанной около прямоугольного треугольника ВКО, лежит на середине гипотенузы ОВ.
Центр описанной около треугольника АВС окружности равноудалён от его вершин,то есть является точкой пересечения серединных перпендикуляров к его сторонам.По условию К - середина ВС. Значит, ОК ⊥ ВС и треугольник ВКО прямоугольный.Центр Р окружности, описанной около прямоугольного треугольника ВКО, лежит на середине гипотенузы ОВ.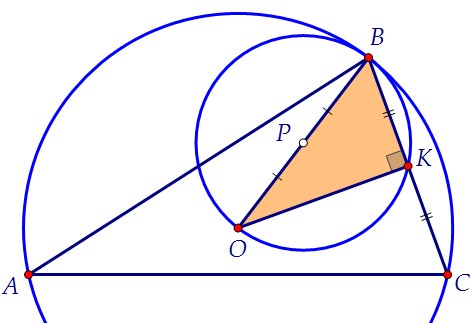 Треугольник ОВТ вписан в ту же окружность. Угол ОТВ прямой, т.к. опирается на полуокружность. Таким образом, ОТ ⊥ АВ.
Треугольник ОВТ вписан в ту же окружность. Угол ОТВ прямой, т.к. опирается на полуокружность. Таким образом, ОТ ⊥ АВ.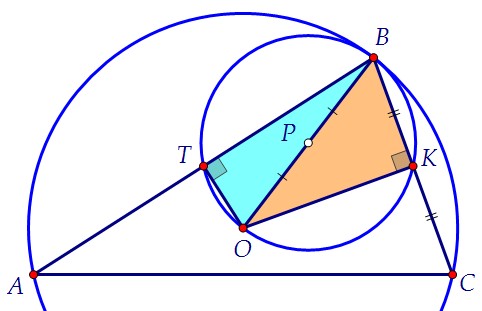 Через точку О проходит единственный перпендикуляр к прямой АВ. Известно,
что это серединный перпендикуляр. Значит, точка Т - середина стороны АВ.
Отрезок ТК - средняя линия треугольника АВС по определению. Значит, ТК || АС по свойству средней линии, ч.т.д.
Через точку О проходит единственный перпендикуляр к прямой АВ. Известно,
что это серединный перпендикуляр. Значит, точка Т - середина стороны АВ.
Отрезок ТК - средняя линия треугольника АВС по определению. Значит, ТК || АС по свойству средней линии, ч.т.д.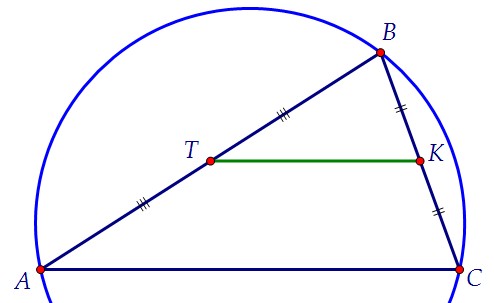 Если средняя линия КТ равна 8, то сторона АС треугольника АВС равно 16.
Если половина стороны АВ равна 6 (ВТ = 6), то вся сторона АВ равна 12.
Если угол ВОК равен 30°, то угол ВОС равен 60°, и дуга ВС равна 60°.
Вписанный угол ВАС равен половине дуги ВС, на которую он опирается.
Если средняя линия КТ равна 8, то сторона АС треугольника АВС равно 16.
Если половина стороны АВ равна 6 (ВТ = 6), то вся сторона АВ равна 12.
Если угол ВОК равен 30°, то угол ВОС равен 60°, и дуга ВС равна 60°.
Вписанный угол ВАС равен половине дуги ВС, на которую он опирается.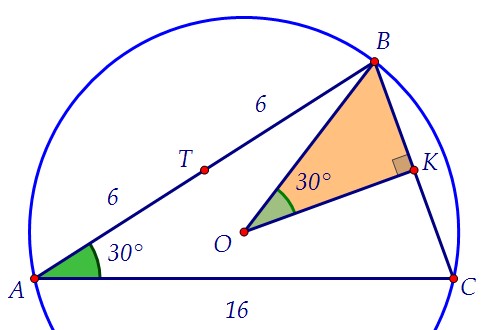 Осталось просто посчитать площадь треугольника АВС:
S = 0,5·AB·AC·sin∠BAC = 0,5·12·16·sin30° = 0,5·12·16·0,5 = 6·8 = 48.Ответ: 48
Осталось просто посчитать площадь треугольника АВС:
S = 0,5·AB·AC·sin∠BAC = 0,5·12·16·sin30° = 0,5·12·16·0,5 = 6·8 = 48.Ответ: 48 Автор: Ольга Себедаш Просмотров: 17203
|

 Центр описанной около треугольника АВС окружности равноудалён от его вершин,то есть является точкой пересечения серединных перпендикуляров к его сторонам.По условию К - середина ВС. Значит, ОК ⊥ ВС и треугольник ВКО прямоугольный.Центр Р окружности, описанной около прямоугольного треугольника ВКО, лежит на середине гипотенузы ОВ.
Центр описанной около треугольника АВС окружности равноудалён от его вершин,то есть является точкой пересечения серединных перпендикуляров к его сторонам.По условию К - середина ВС. Значит, ОК ⊥ ВС и треугольник ВКО прямоугольный.Центр Р окружности, описанной около прямоугольного треугольника ВКО, лежит на середине гипотенузы ОВ. Треугольник ОВТ вписан в ту же окружность. Угол ОТВ прямой, т.к. опирается на полуокружность. Таким образом, ОТ ⊥ АВ.
Треугольник ОВТ вписан в ту же окружность. Угол ОТВ прямой, т.к. опирается на полуокружность. Таким образом, ОТ ⊥ АВ. Через точку О проходит единственный перпендикуляр к прямой АВ. Известно,
что это серединный перпендикуляр. Значит, точка Т - середина стороны АВ.
Отрезок ТК - средняя линия треугольника АВС по определению. Значит, ТК || АС по свойству средней линии, ч.т.д.
Через точку О проходит единственный перпендикуляр к прямой АВ. Известно,
что это серединный перпендикуляр. Значит, точка Т - середина стороны АВ.
Отрезок ТК - средняя линия треугольника АВС по определению. Значит, ТК || АС по свойству средней линии, ч.т.д. Если средняя линия КТ равна 8, то сторона АС треугольника АВС равно 16.
Если половина стороны АВ равна 6 (ВТ = 6), то вся сторона АВ равна 12.
Если угол ВОК равен 30°, то угол ВОС равен 60°, и дуга ВС равна 60°.
Вписанный угол ВАС равен половине дуги ВС, на которую он опирается.
Если средняя линия КТ равна 8, то сторона АС треугольника АВС равно 16.
Если половина стороны АВ равна 6 (ВТ = 6), то вся сторона АВ равна 12.
Если угол ВОК равен 30°, то угол ВОС равен 60°, и дуга ВС равна 60°.
Вписанный угол ВАС равен половине дуги ВС, на которую он опирается. Осталось просто посчитать площадь треугольника АВС:
S = 0,5·AB·AC·sin∠BAC = 0,5·12·16·sin30° = 0,5·12·16·0,5 = 6·8 = 48.Ответ: 48
Осталось просто посчитать площадь треугольника АВС:
S = 0,5·AB·AC·sin∠BAC = 0,5·12·16·sin30° = 0,5·12·16·0,5 = 6·8 = 48.Ответ: 48