Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

15(C3). Решите логарифмическое неравенство (вар. 90)

Решите неравенство:

${log_{(2-5x)}{3}+\frac{1}{log_{2}{(2-5x)}}}\leq{\frac{1}{log_{6}{(6x^2-6x+1)}}}$

Сначала равносильно преобразуем неравенство:

${log_{(2-5x)}{3}+log_{(2-5x)}{2}}\leq{log_{(6x^2-6x+1)}{6}}$

${log_{(2-5x)}{6}}\leq{log_{(6x^2-6x+1)}{6}}$

Исследуем последнее неравенство (числа под знаками логарифма равны).

1) Пусть оба основания больше единицы (обе функции возрастают).

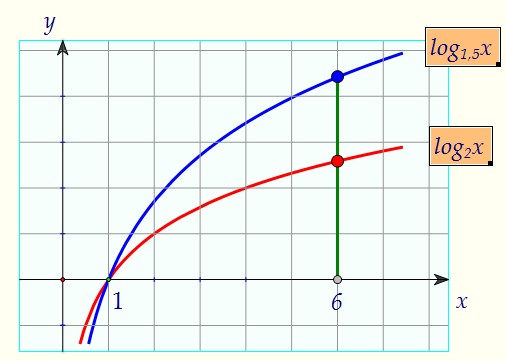17(C3). Решите логарифмическое неравенство (вар. 90)

Тогда первое основание должно быть не меньше второго.
Достаточно решить систему неравенств:

$\left\{ \begin{array}{rcl} 6x^2-6x+1>1 \\ {2-5x}\geq{6x^2-6x+1}\\ \end{array} \right$

$\left\{ \begin{array}{rcl} x^2-x>0 \\ {6x^2-x-1}\leq{0}\\ \end{array} \right$

$\left\{ \begin{array}{rcl} x(x-1)>0 \\ {(3x+1)(2x-1)}\leq{0}\\ \end{array} \right$

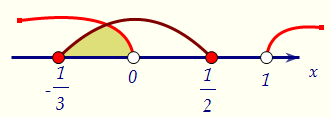17(C3). Решите логарифмическое неравенство (вар. 90)

2) Оба основания находятся от нуля до единицы (обе функции убывают).

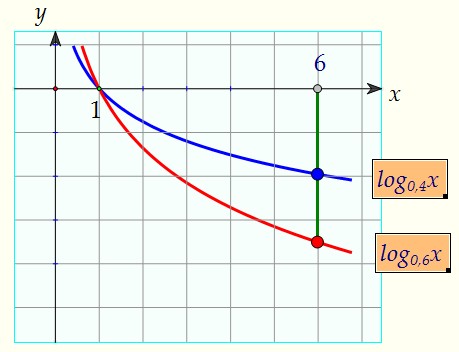И здесь первое основание должно быть не меньше второго.
Достаточно решить систему неравенств:

$\left\{ \begin{array}{rcl} 6x^2-6x+1>0 \\ 2-5x<1 \\ {2-5x}\geq{6x^2-6x+1}\\ \end{array} \right$

$\left\{ \begin{array}{rcl} 6x^2-6x+1>0 \\ x>0,2 \\ {6x^2-x-1}\leq0\\ \end{array} \right$

Корнями трёхчлена 6х² - 6х + 1 являются числа:

$\frac{3-\sqrt{3}}{6}$ и $\frac{3+\sqrt{3}}{6}$

Оба они положительны и находятся по разные стороны от 0,5.
Необходимо меньший из них сравнить с числом 0,2.

$\frac{1}{5}$            .................             $\frac{3-\sqrt{3}}{6}$

$6$           .................           $15-5\sqrt{3}$

$5\sqrt{3}$       .................           $9$

$75$          .................           $81$

Так как 81 > 75, то меньший корень больше, чем 0,2.

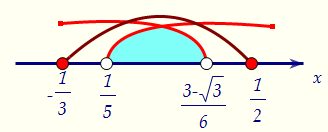17(C3). Решите логарифмическое неравенство (вар. 90)

3) Пусть одна из функций возрастает, а другая убывает.

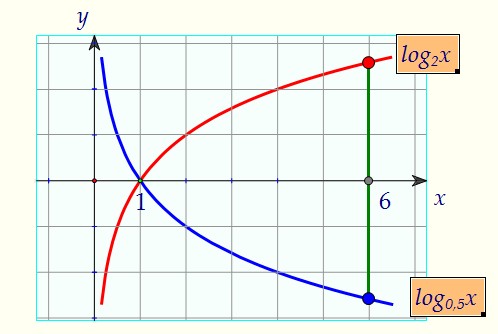Положительное число всегда больше отрицательного, поэтому чтобы
неравенство выполнялось, именно первая функция должна убывать.
Достаточно решить систему неравенств:

$\left\{ \begin{array}{rcl} 6x^2-6x+1>1 \\ 0<2-5x<1 \\ \end{array} \right$

$\left\{ \begin{array}{rcl} x(x-1)>0 \\ 0,2<x<0,4 \\ \end{array} \right$

Эта система решений не имеет. В ответ пишем первые два результата.

$[-\frac{1}{3}; 0); (\frac{1}{5};\frac{3-\sqrt{3}}{6})$