Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Хорда AB стягивает дугу окружности, равную 120°. Точка С лежит на этой
дуге, а точка D лежит на хорде AB. При этом AD = 2, BD = 1, DC = √2.
а) Докажите, что угол ADC равен π/6.
б) Найдите площадь треугольника ABC.



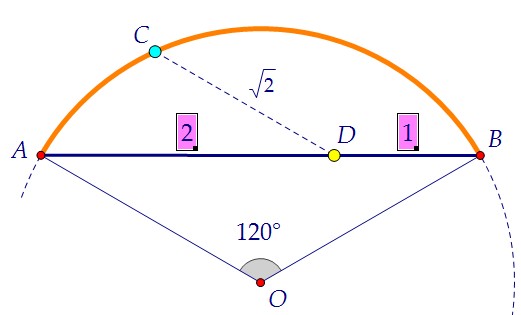Исследуем поэтапно условие задачи. Логически пройдём от пункта к пункту.

1) Из равнобедренного треугольника АОВ тут же найдём R = OA = OB = √3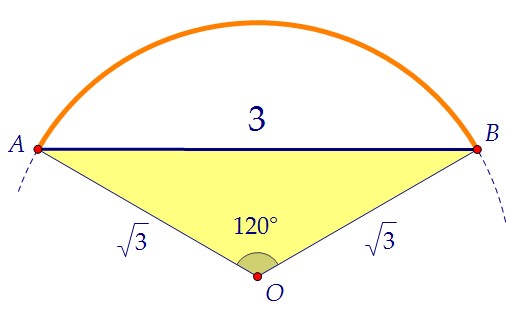



2) Воспользуемся свойством пересекающихся хорд окружности АВ и CF.
Зная оба кусочка первой и один кусочек второй, найдём недостающий.



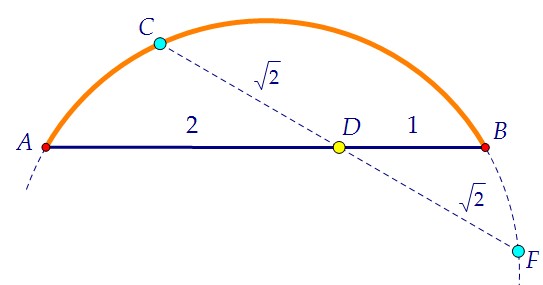3) Оказалось, что точка D - середина хорды CF. А значит, OD ⊥ CF.



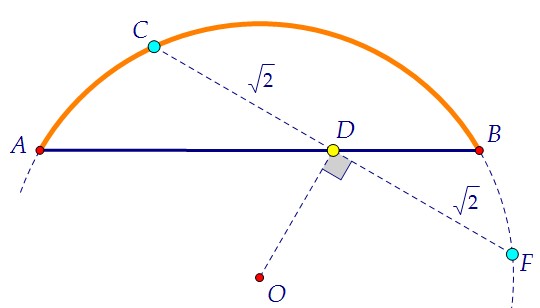4) Из треугольника COD, зная катет и гипотенузу, находим OD = 1.



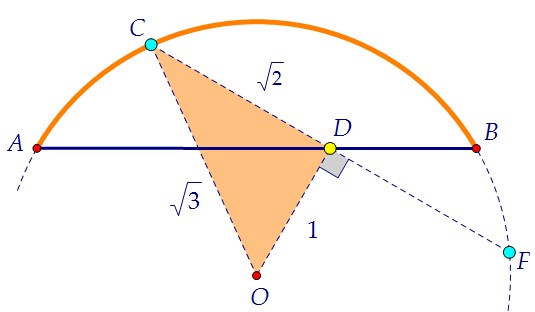5) Стороны треуг. ODB равны 1, 1 и √3. Значит, углы его 120°, 30° и 30°.



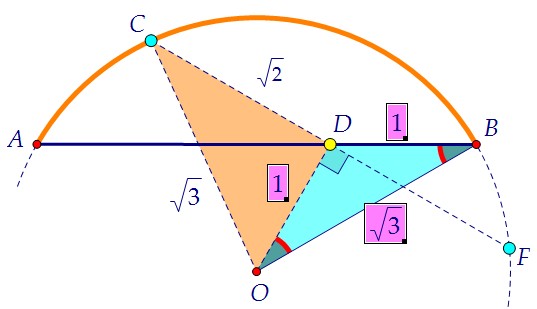6) ∠BDF = 120° - 90° = 30°, ∠ADC = ∠BDF = 30° (как вертикальные)



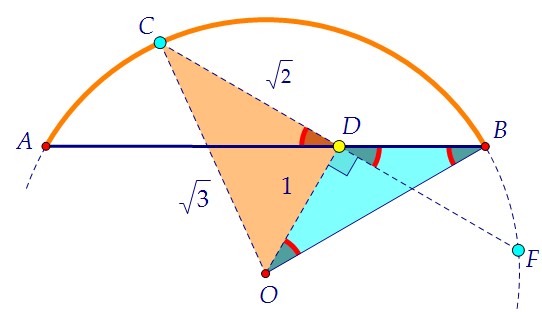7) Проведём высоту СР треугольника АВС и найдём её из треугольника РСD.



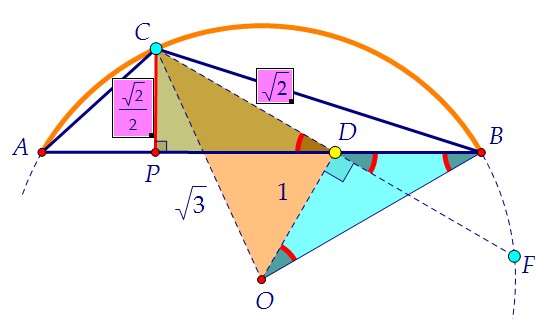8) Осталось найти площадь треугольника АВС:

Автор: Ольга Себедаш             Просмотров: 17304