Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

а) Школьники одного класса в сентябре ходили в два туристических похода.
В первом походе мальчиков было меньше 2/5 общего числа участников этого
похода, во втором – тоже меньше 2/5. Докажите, что в этом классе мальчики
составляют меньше 4/7 общего числа учеников, если известно, что
каждый из учеников участвовал по крайней мере в одном походе.

Сделаем так, чтобы доля мальчиков оказалась наибольшей из всех возможных.
1) Тогда в каждом походе их доля составит ровно 2/5 и никак не меньше.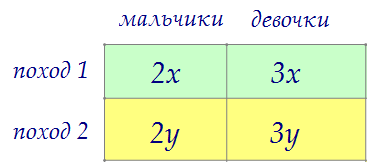



2) Для достижения данной цели, каждого мальчика отправим только в один поход.
3) Доля девочек от общего числа участников должна оказаться как можно меньше.
    Это значит, что каждая девочка должна побывать в каждом из двух походов.
    Получаем, что 3x = 3y, а значит, x = y. Считаем общее число участников.



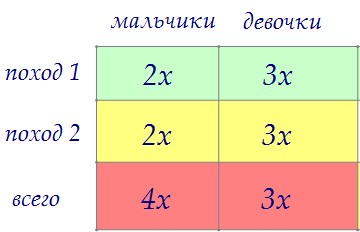Это и означает, что максимальная доля мальчиков составляет 4/7 от числа учеников.

===========================================

Решим эту задачу в общем виде для двух походов, используя коэффициенты p и k.
(вместо данных в исходной задаче коэффициентов 2/5 и 2/5)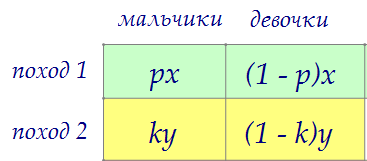



Рассуждая точно таким же образом, получаем:





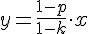Число девочек, которые участвовали в походах:



Считаем общее число мальчиков - участников:



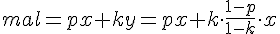Поделим число всех мальчиков на всех девочек:



Постепенно преобразовывая, найдём нужную долю:









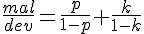
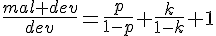
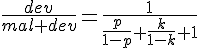
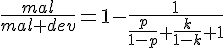Результат можно развить для любого числа походов:

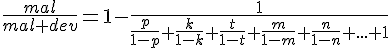Автор: Ольга Себедаш             Просмотров: 9115