|
Сфера единичного радиуса вписана в двугранный угол величиной 60ᵒ.
В тот же угол вписана сфера меньшего радиуса так, что она касается предыдущей. Угол между прямой а, соединяющей центры обеих сфер, и ребром двугранного угла составляет 45°.
а) Постройте плоскость, проходящую через ребро двугранного угла и прямую а.
б) Найдите радиус меньшей сферы.
Вот первая картинка, которая приходит в голову после чтения двух первых фраз.Здесь изображено сечение двух касающихся сфер, вписанных в двугранный угол,
плоскостью, перпендикулярной ребру двугранного угла (ребро видим как точку В).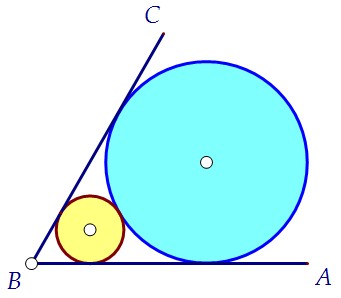 Но прямая, соединяющая центры сфер, здесь, очевидно, перпендикулярна ребру.Поэтому в нашем случае одна из сфер будет находиться ЗА другой, ПОЗАДИ неё.И обе плоскости, перпендикулярные ребру и проходящие каждая через центр своей сферы, будут разными, но при этом параллельными друг другу.
Но прямая, соединяющая центры сфер, здесь, очевидно, перпендикулярна ребру.Поэтому в нашем случае одна из сфер будет находиться ЗА другой, ПОЗАДИ неё.И обе плоскости, перпендикулярные ребру и проходящие каждая через центр своей сферы, будут разными, но при этом параллельными друг другу.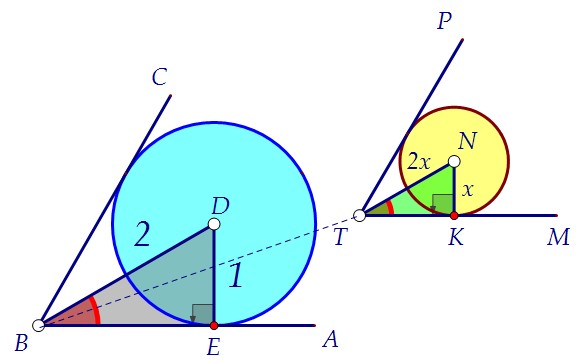 А учитывая тот факт, что центр вписанной окружности лежит на биссектрисе угла,а угол равен 60°, мы получаем прямоугольные треугольники с острым углом 30°.И делаем первый замечательный вывод: расстояние от центров окружностей до ребра двугранного угла в два раза больше их соответствующих радиусов.Теперь рассмотрим другое сечение - биссекторной плоскостью двугранного угла.
Т.к. шары вписаны в двугранный угол, то их центры равноудалены от его граней
и поэтому лежат на биссекторной плоскости (прямая SВ - ребро дв. угла).
А учитывая тот факт, что центр вписанной окружности лежит на биссектрисе угла,а угол равен 60°, мы получаем прямоугольные треугольники с острым углом 30°.И делаем первый замечательный вывод: расстояние от центров окружностей до ребра двугранного угла в два раза больше их соответствующих радиусов.Теперь рассмотрим другое сечение - биссекторной плоскостью двугранного угла.
Т.к. шары вписаны в двугранный угол, то их центры равноудалены от его граней
и поэтому лежат на биссекторной плоскости (прямая SВ - ребро дв. угла).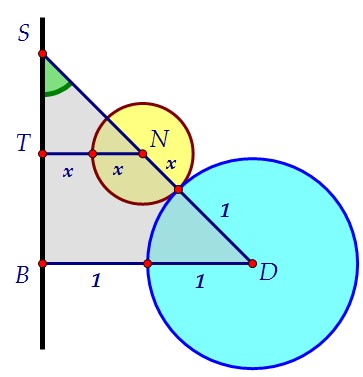 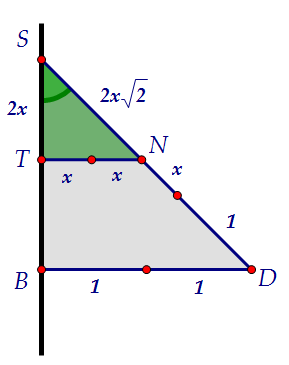 На рисунке учтен первый вывод о расстоянии от центров шаров до ребра SB.
Образовавшийся прямоугольный треугольник - равнобедренный по условию.
Гипотенуза такого треугольника в √2 раз больше катета. х - маленький радиус.SN = 2x√2SD = 2√2DN = 2√2 - 2х√2С другой стороны, DN = х + 1. Получаем, что2√2 - 2х√2 = х + 1х(1 + 2√2) = 2√2 - 1Осталось разделить и преобразовать:
На рисунке учтен первый вывод о расстоянии от центров шаров до ребра SB.
Образовавшийся прямоугольный треугольник - равнобедренный по условию.
Гипотенуза такого треугольника в √2 раз больше катета. х - маленький радиус.SN = 2x√2SD = 2√2DN = 2√2 - 2х√2С другой стороны, DN = х + 1. Получаем, что2√2 - 2х√2 = х + 1х(1 + 2√2) = 2√2 - 1Осталось разделить и преобразовать: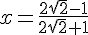 (2\sqrt{2}-1)}{(2\sqrt{2}+1)(2\sqrt{2}-1)}) 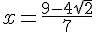 И для наглядности симпатичная картинка, найденная на просторах интернета. Центр шара, вписанного в двугранный угол, лежит на биссекторной плоскости. И для наглядности симпатичная картинка, найденная на просторах интернета. Центр шара, вписанного в двугранный угол, лежит на биссекторной плоскости.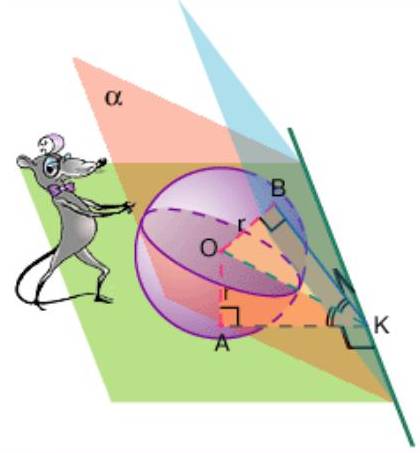 Автор: Ольга Себедаш Просмотров: 13758
|

 Но прямая, соединяющая центры сфер, здесь, очевидно, перпендикулярна ребру.Поэтому в нашем случае одна из сфер будет находиться ЗА другой, ПОЗАДИ неё.И обе плоскости, перпендикулярные ребру и проходящие каждая через центр своей сферы, будут разными, но при этом параллельными друг другу.
Но прямая, соединяющая центры сфер, здесь, очевидно, перпендикулярна ребру.Поэтому в нашем случае одна из сфер будет находиться ЗА другой, ПОЗАДИ неё.И обе плоскости, перпендикулярные ребру и проходящие каждая через центр своей сферы, будут разными, но при этом параллельными друг другу. А учитывая тот факт, что центр вписанной окружности лежит на биссектрисе угла,а угол равен 60°, мы получаем прямоугольные треугольники с острым углом 30°.И делаем первый замечательный вывод: расстояние от центров окружностей до ребра двугранного угла в два раза больше их соответствующих радиусов.Теперь рассмотрим другое сечение - биссекторной плоскостью двугранного угла.
Т.к. шары вписаны в двугранный угол, то их центры равноудалены от его граней
и поэтому лежат на биссекторной плоскости (прямая SВ - ребро дв. угла).
А учитывая тот факт, что центр вписанной окружности лежит на биссектрисе угла,а угол равен 60°, мы получаем прямоугольные треугольники с острым углом 30°.И делаем первый замечательный вывод: расстояние от центров окружностей до ребра двугранного угла в два раза больше их соответствующих радиусов.Теперь рассмотрим другое сечение - биссекторной плоскостью двугранного угла.
Т.к. шары вписаны в двугранный угол, то их центры равноудалены от его граней
и поэтому лежат на биссекторной плоскости (прямая SВ - ребро дв. угла).
 На рисунке учтен первый вывод о расстоянии от центров шаров до ребра SB.
Образовавшийся прямоугольный треугольник - равнобедренный по условию.
Гипотенуза такого треугольника в √2 раз больше катета. х - маленький радиус.SN = 2x√2SD = 2√2DN = 2√2 - 2х√2С другой стороны, DN = х + 1. Получаем, что2√2 - 2х√2 = х + 1х(1 + 2√2) = 2√2 - 1Осталось разделить и преобразовать:
На рисунке учтен первый вывод о расстоянии от центров шаров до ребра SB.
Образовавшийся прямоугольный треугольник - равнобедренный по условию.
Гипотенуза такого треугольника в √2 раз больше катета. х - маленький радиус.SN = 2x√2SD = 2√2DN = 2√2 - 2х√2С другой стороны, DN = х + 1. Получаем, что2√2 - 2х√2 = х + 1х(1 + 2√2) = 2√2 - 1Осталось разделить и преобразовать: